Question

В трапеции ABCD AB и CD - основания. AB=3,BC=9,CD=15,AD=7. Найдите наименьшее значение суммы AC+BD.

Answer 1

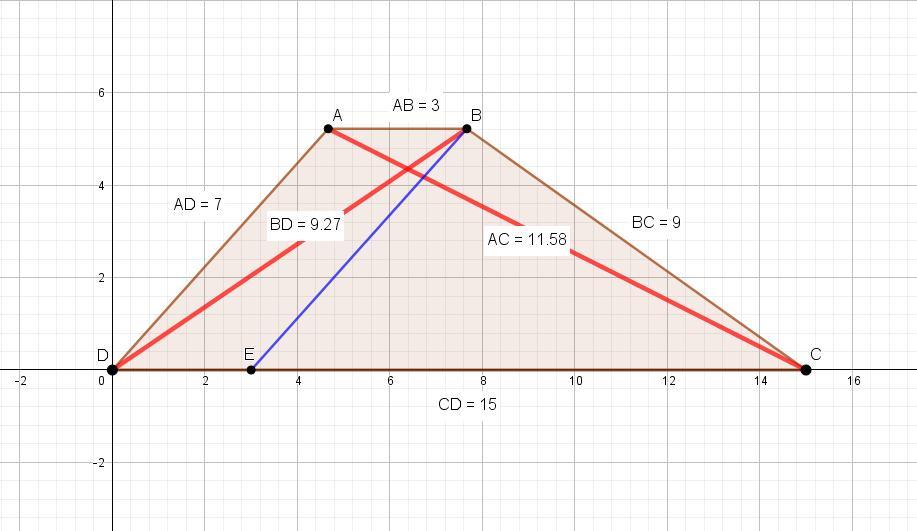
Дана трапеция ABCD AB и CD - основания. AB=3,BC=9,CD=15,AD=7.

Из точки В проводим отрезок ВЕ, равный и параллельный AD.

Получим треугольник ВСЕ с основанием СЕ = 15 - 3 = 12.

По теореме косинусов находим косинусы углов при основании этого треугольника, которые равны косинусам углов при основании трапеции.

cos A = 0,666666667 cos B = -0,111111111 cos С = 0,814814815

Аrad = 0,841068671 Brad = 1,682137341 Сrad = 0,618386642

Аgr = 48,1896851 Bgr = 96,37937021 Сgr = 35,43094469.

Далее по этим косинусам и сторонам трапеции находим диагонали.

Известно: две стороны а , в и угол между ними С.        

Диагональ d2 равна :

  a b     d2             С градус     С радиан

  7 15 11,5758369   48,1896851     0,841068671.

Известно: две стороны а , в и угол между ними D.        

Диагональ d1 равна :

  a b      d1              D градус       D радиан

  9 15 9,273618495     35,43094469 0,618386642.

Answer 2

Ответ:

9√86

Объяснение:

BK, AN⊥AD⇒BK=AN, KN=AB=3

CK=x⇒ND=12-x

BC²-CK²=BK²=AN²=AD²-ND²

BC²-CK²=AD²-ND²

7²-x²=9²-(12-x)²

49-x²=81+24x-x²-144

24x=112

CK=x=14/3

CN=3+x=23/3; DK=12-x=22/3

AN²=BK²=7²-(14/3)²=49-196/9=245/9

AC²=AN²+CN²=245/9+(23/3)²=245/9+529/9=774/9=86⇒AC=√86

BD²=BK²+DK²=245/9+(22/3)²=245/9+484/9=774/9=81⇒BD=9

AC+BD=9+√86