Предмет: Геометрия,
автор: Rewsa
В прямоугольном треугольнике один из острых углов равен 30°. Высота, проведенная из вершины прямого угла к гипотенузе равна 2 см. Найти больший катет данного прямоугольного треугольника.
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
дивись файл:
Приложения:

Автор ответа:
1
Ответ: 4 cм .
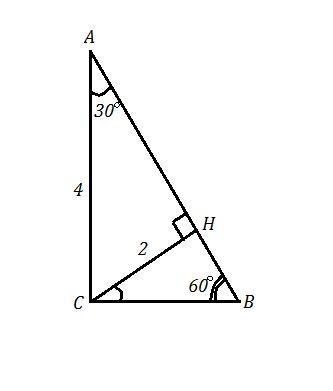
ΔАВС , ∠С=90° , СН⊥АВ , СН=2 см , ∠А=30°
Найти бОльший катет .
Рассмотрим ΔАСН . ∠АНС=90° , ∠А=30° ⇒ катет против угла в 30° равен половине гипотенузы , то есть СН=1/2*АС ⇒ АС=2*СН=2*2=4 см
Так как ∠В=180°-90°-30°=60° , ∠В >∠A .
Против бОльшего угла лежит бОльший катет. Поэтому бОльший катет лежит против ∠В , а это катет АС=4 см .
Можно проверить, что катет ВС=АС*tg30=4*(1/√3)=4/√3≈2,31 см , BC<AC .
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: Cona564
Предмет: Русский язык,
автор: Romannnn5
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: AmiR4IKBross
Предмет: Алгебра,
автор: bublikovaivetta