Предмет: Математика,
автор: Аноним
Помогите решить задачку, пожалуйста. ДАМ 50 БАЛЛОВ!!!
Приложения:

Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
y = x² +b - это парабола ветвями вверх
y = 2x-2 - это прямая наклоном влево и смещением по оси у на -2
если они имеют только одну общую точку, значит у = 2х-2 - это касательная к у = x² +b в точке х₀
уравнение касательной
у нас
и будет касательная
а мы знаем, что коэффициент при х у касательной =2
(потому как Ук= 2*х -2)
и вот тогда
2х₀=2 и х₀ = 1 - это абсцисса той самой одной общей точки
и тогда найдем b из условия, что графики функций имеют одну общую точку
и у нас функция имеет вид
y(x) = x² -1 и y(1) = 0 это ордината одной общей точки
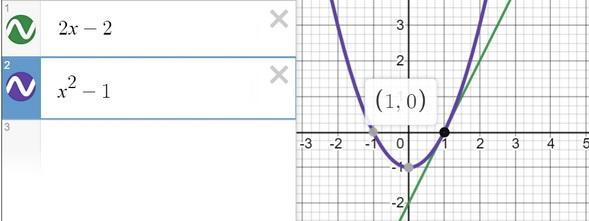
и мы получили точку касания (1; 0) - это и есть координаты одной общей точки двух графиков
на рисунке графики и одна общая точка
Приложения:
pushpull:
https://matematikam.ru/calculate-online/grafik.php
Похожие вопросы
Предмет: Русский язык,
автор: abubekerova2016
Предмет: Русский язык,
автор: narine2728
Предмет: Русский язык,
автор: аовоослылоыокиоаоы
Предмет: Алгебра,
автор: Yararei
Предмет: Биология,
автор: PolinaCat29