Question

Положительные числа x и y таковы, что x+2y=6. Найдите наибольшее возможное значение выражения xy

Answer 1

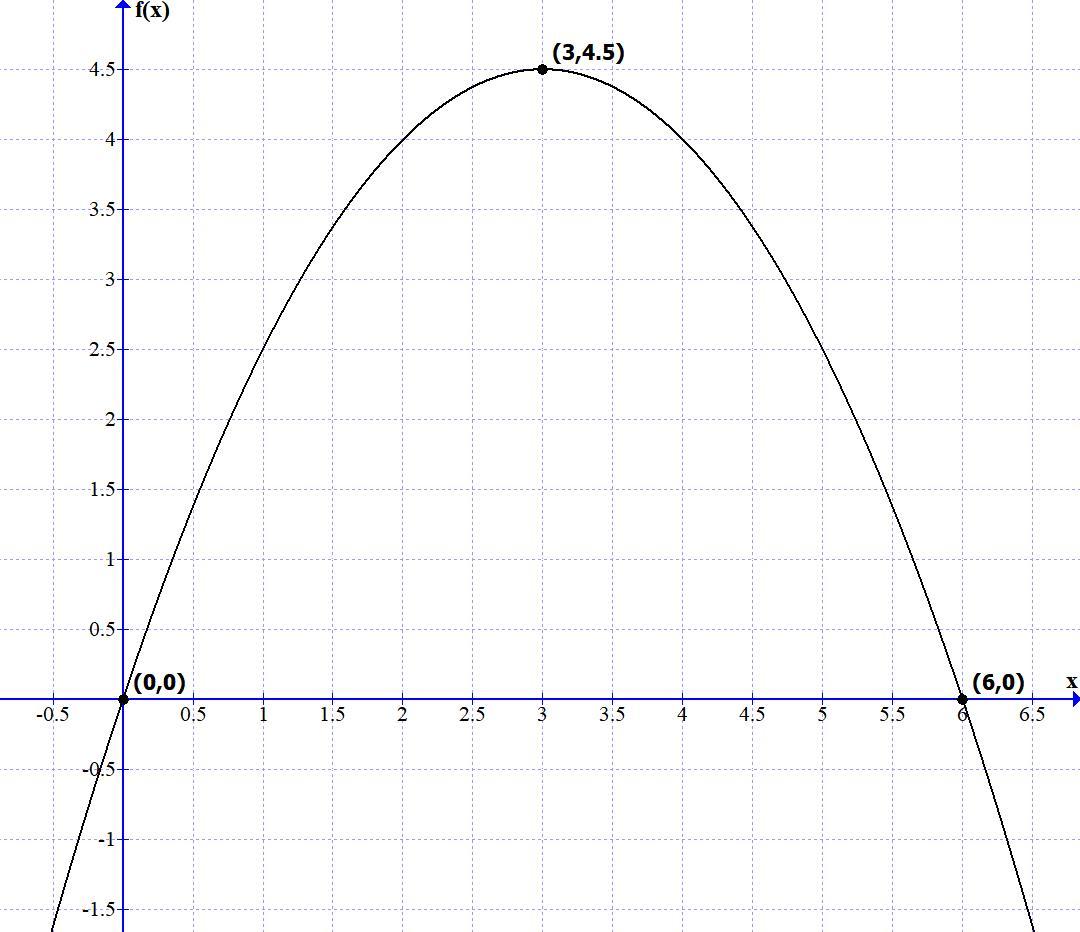
Решение сводится к нахождению вершины параболы (см.ниже).

Для начала, из уравнения

x+2y=6

выразим игрек:

y=3-0,5x

И подставим это выражение в произведение xy.

Получим такую функцию:

f(x) = xy = x(3-0,5x) = -0,5x²+3x

Эта функция показывает, как меняется значение произведения xy при изменении переменной икс (и, соответствующего ему изменения игрек, ведь они связаны указанным в задаче уравнением).

График этой функции- это парабола, ветви которой уходят вниз. А верхняя точка (максимум)- это вершина параболы.

Координату икс вершины можно вычислить как среднее арифметическое между иксами в нулях функции.

Нули функции (точки, в которых функция равна нулю) будут при:

x₁=0  и  3-0,5x = 0,  то есть при x₂=6

Среднее равно x₀=(0+6)/2=3

При этом, функция будет равна:

f(3) = -0,5*3²+3*3 = 4,5

Это и есть наше искомое максимальное значение произведения xy.

Ответ: 4,5

Answer 2

https://znanija.com/task/45137756

Положительные числа x и y таковы, что x+2y=6. Найдите наибольшее возможное значение выражения xy .

Ответ:   4,5

Объяснение:  Сразу можно применить неравенство  Коши:  Среднее геометрическое неотрицательных чисел меньше или равно среднему арифметическому этих чисел .

* * * √(ab)  ≤  (a+b) / 2 ,если  a≥ 0 и b ≥ 0 притом равенство (т.е. максимальное значение ab получается , если a=b * * *

В данном  примере  a = x > 0 , b =2y > 0

   √(x*2y)  ≤ ( x+2y) / 2  равенство выполняется, если x=2y.  

Из  x+2y=6  следует   x =2y =3   иначе   x =3 ; y =1,5.

max(x*y) = 3*(3/2) = 4,5 .