Question

Найдите все значения а, при которых система уравнений имеет ровно три различных решения.

Answer 1

Ответ:

Пошаговое объяснение:

первое уравнение распадается на 2

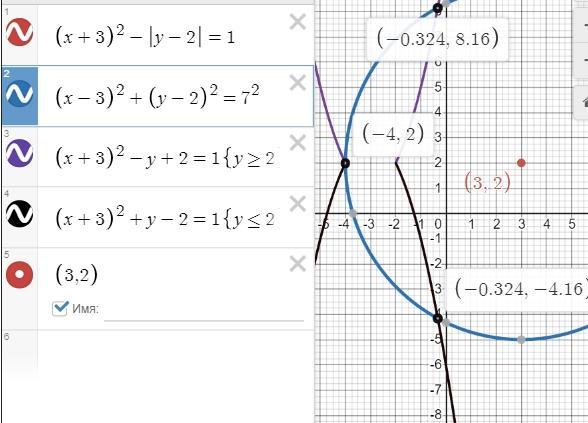
(x+3)² -y+2=1  для у ≥ 2 ,т.е. для верхних ветвей параболы

(x+3)²+y -2 =1  для у ≤ -2, т.е для нижних ветвей параболы

пересекаются эти параболы в точках (-4; 2) и (-2;2)

второе уравнение - окружность с центром в точке (3; 2)

для того, чтобы окружность имела 3 общие точки с такой вот обрезанной параболой, состоящей из двух частей, нужно, чтобы окружность пересекла правую часть, и коснулась левой.

т.е. надо, чтобы окружность имела радиус 3-(-4) = 7

тогда а²-4а+13=49

а² -4а -36 =0 (здесь дискриминант D=160= 4√(10)

и тогда корни уравнения

а₁=2+2√(10)       а₂ = 2-2√(10)