Question

Помогите пожалуйста!

Answer 1

Ответ:

OO₁=30,75

Объяснение:

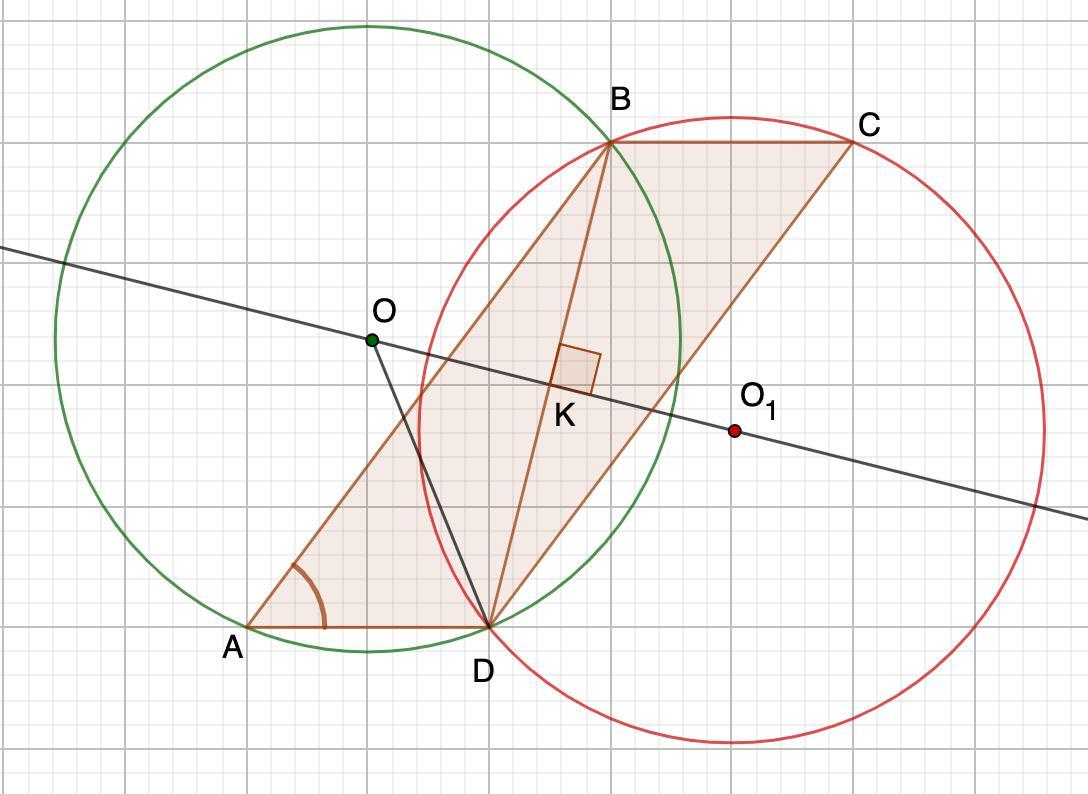
Линия центров пересекающихся окружностей делит общую хорду пополам и перпендикулярна ей.

Диагональ параллелограмма делит его на два равных треугольника.

Противоположные стороны параллелограмма равны.

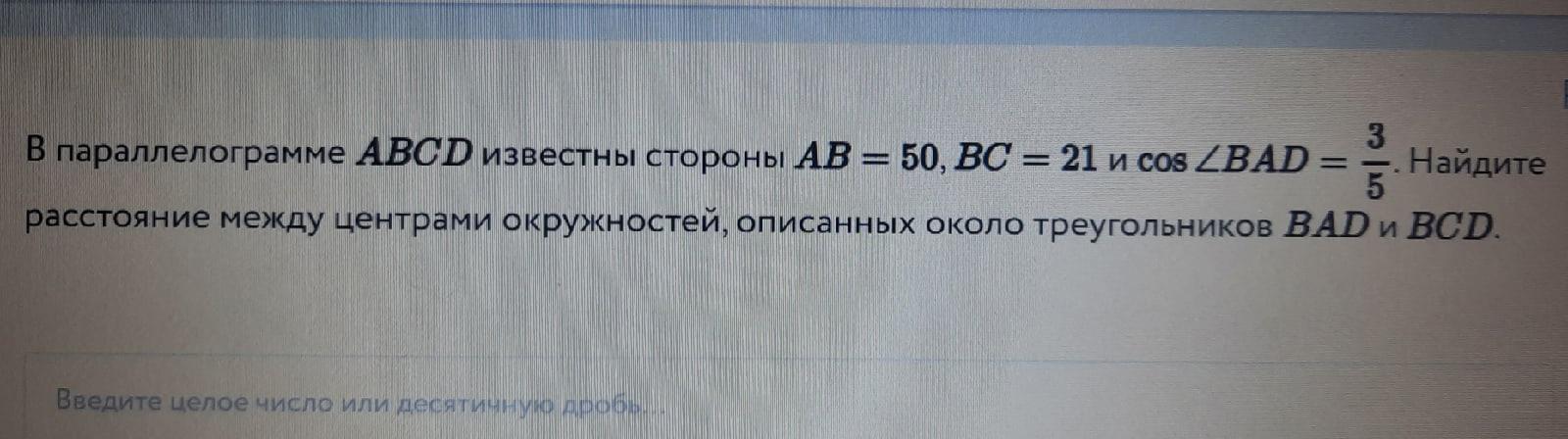
Дано: ABCD - параллелограмм.

АВ = 50; ВС=21; cos∠BAD= 3/5

Окр. ОR и O₁R - описанные около ΔBAD и ΔBCD соответственно.

Найти: ОО₁

Решение:

1. По теореме косинусов найдем диагональ BD.

BD²=АВ²+AD²-2·AB·AD·cos∠BAD

$BD^2=50^2+21^2-2*50*21*\frac{3}{5} =1681\\BD=41$

2) Выразим sin∠BAD, зная cos∠BAD.

Используем основное тригонометрическое тождество:

$sin^2\alpha +cos^2\alpha =1\\sin^2\angle{BAD}=1-\frac{9}{25} =\frac{16}{25}\\sin\angle{BAD }=\frac{4}{5}$

3) Так как ΔBAD = ΔBCD, то у описанных окружностей будут одинаковые радиусы R.

По теореме синусов найдем R:

$R=\frac{BD}{2sin\angle{BAD}} =\frac{41*5}{2*4} =25,625$

4. Рассмотрим ΔOKD - прямоугольный.

DK=41:2=20,5

По теореме Пифагора:

$OK=\sqrt{25,625^2-20,5^2}=15,375$

⇒ OO₁=15,375·2=30,75