Предмет: Алгебра,
автор: yanona96
2sin^3x - cos2x -sinx=0 помогите пожалуйста решить)
Ответы
Автор ответа:
0
Решение:
2sin^3x-cos2x-sinx=0
sinx(2sin^2x-1)-cos2x=0
-sinxcos2x-cos2x=0
-cos2x(sinx+1)=0
cos2x=0
2x=п/2(2k+1)
x=п/4(2k+1)
sinx=-1
x=-П/2+2пk
2sin^3x-cos2x-sinx=0
sinx(2sin^2x-1)-cos2x=0
-sinxcos2x-cos2x=0
-cos2x(sinx+1)=0
cos2x=0
2x=п/2(2k+1)
x=п/4(2k+1)
sinx=-1
x=-П/2+2пk
Автор ответа:
0
//////////////////////////////////////////////////////////////////
Приложения:
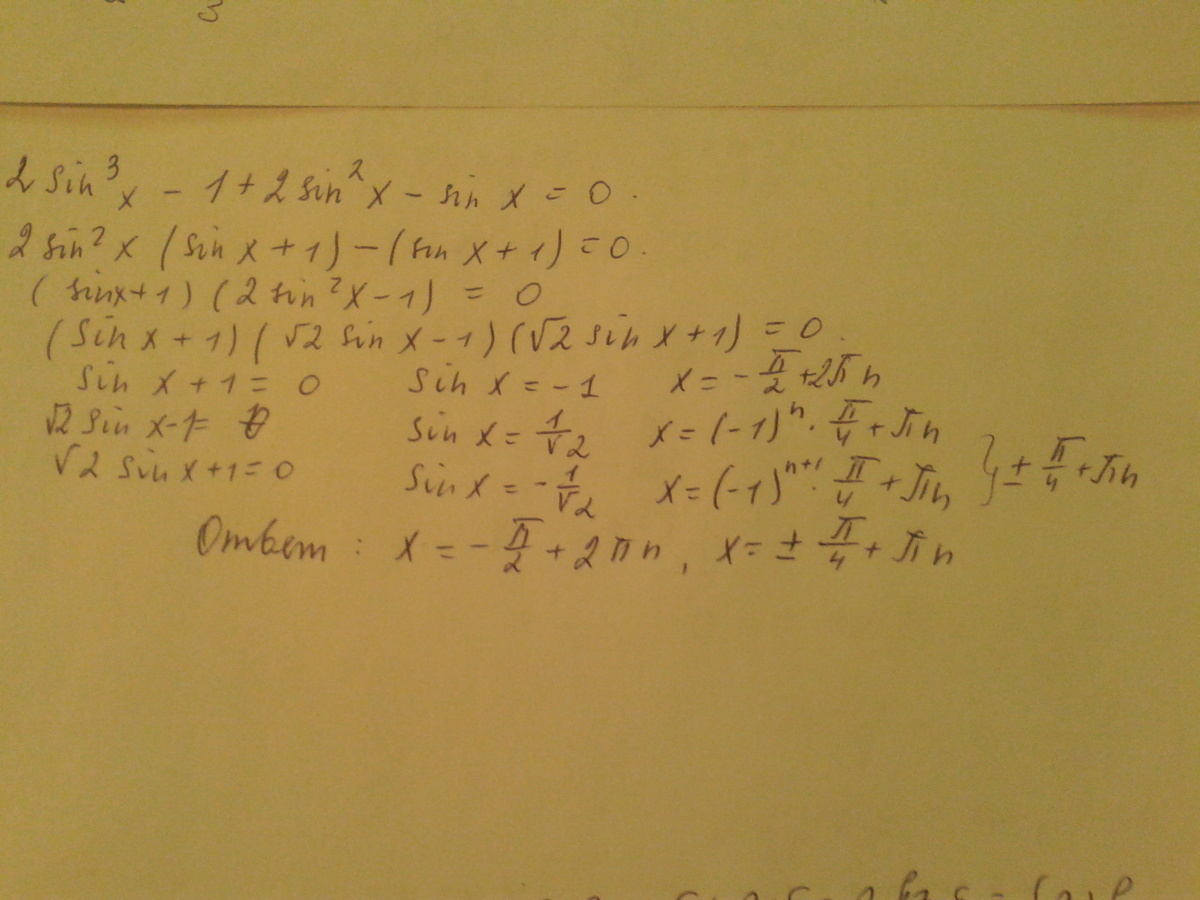
Похожие вопросы
Предмет: Английский язык,
автор: bektursynsafiie
Предмет: Биология,
автор: ajmerialieva4
Предмет: Математика,
автор: serikajym26
Предмет: Физика,
автор: cергей1998