Question

В треугольнике ABC сторона BC равна a. Точка F — середина AB, I — точка пересечения биссектрис
треугольника ABC. Оказалось, что ∠AIF = ∠ACB. Найдите периметр треугольника ABC.

Answer 1

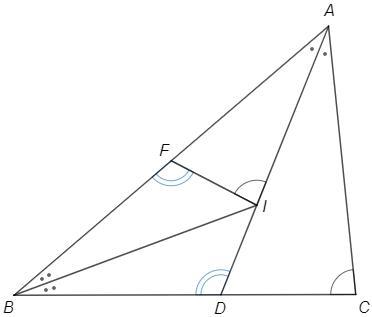
См. чертеж

Пусть BM II IF; где точка M - пересечение BM и AI.

∠BMA = ∠FIA = ∠BCA; => M лежит на описанной окружности (ABC).

так как AM - биссектриса ∠BAC, то M - центр окружности трезубца.

=> BM = MI = MC;

так как IF - средняя линия △BAM, то FI = BM/2, и AI = IM (= BM = MC; !)

Гомотетия H(A, 1/2) переводит  M-> I; B -> F; окружность (ABC) -> (AFI);

и точку C переводит в середину AC - точку L;

=> L лежит на (AFI); IL II MC; IL = MC/2;

=> IL = FI;

Если E и K - точки касания вписанной окружности со сторонами AB и AC соответственно, то

△IEF = △IKL ( прямоугольные теругольники с равными катетами и гипотенузами, катеты - это радиусы вписанной окружности, а равенство гипотенуз только что доказано: IL = FI)

=> IF = KL;

пусть BC = a (как в условии), AB =c; AC = b; p = (a + b + c)/2; как обычно.

тогда AE = AK = p - a; (касательные к вписанной окружности из точки A)

=> c/2 - (p - a) = (p - a) - b/2;

2p - 2a = (b + c)/2 = p - a/2; => p = 3a/2;

ну, а периметр равен 2p = 3a;

этот ответ легко проверятеся, так как условие работает для равностороннего треугольника.

Answer 2

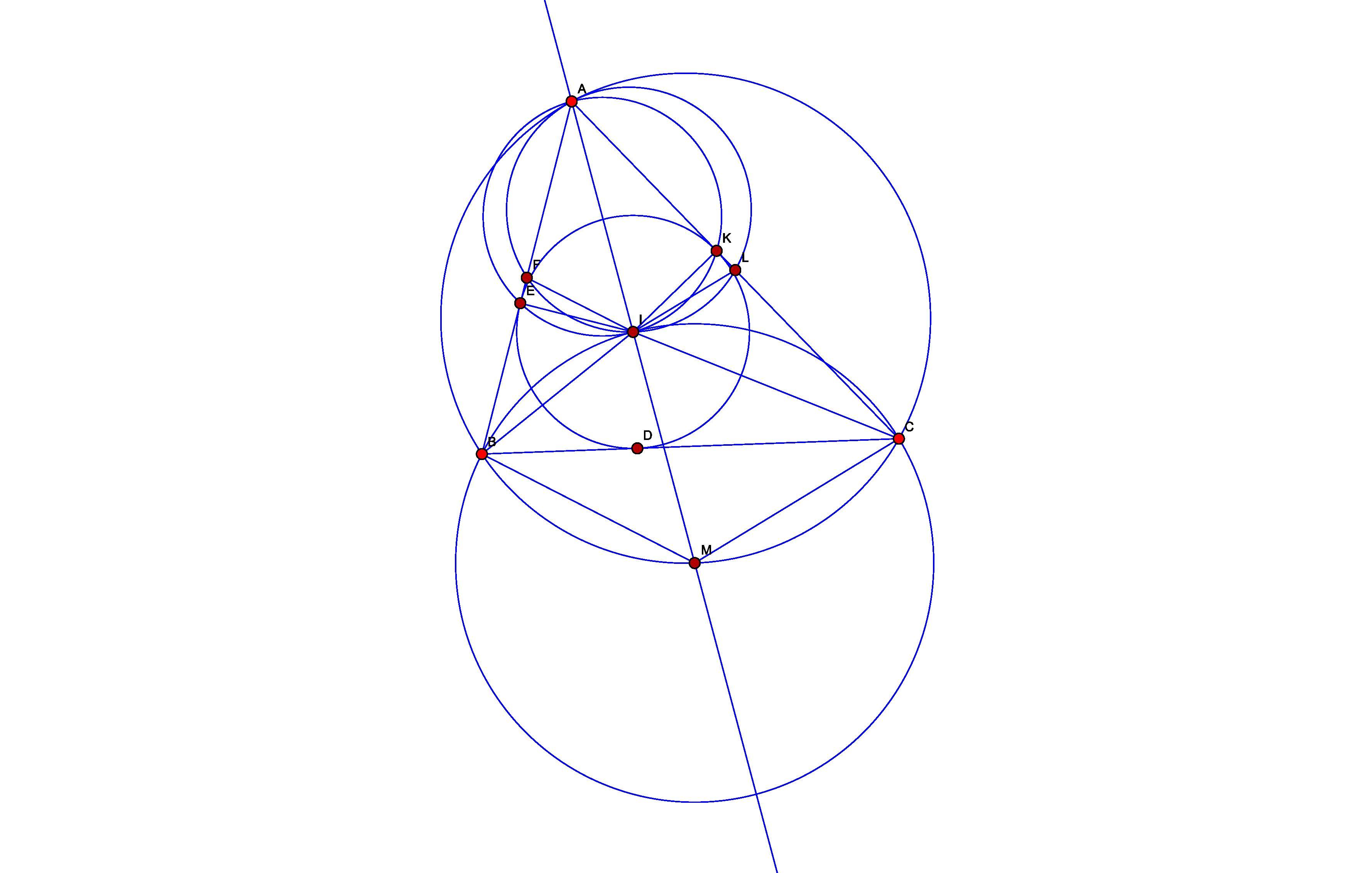
AD - биссектриса

△AIF~△ACD (по двум углам) => ∠BFI=∠BDI

△BFI=△BDI (по стороне и прилежащим углам) => BD=BF => AB=2BD

AB/BD =AC/DC (т о биссектрисе) => AC=2DC

P(ABC) =AB+AC+BC =2BD +2DC +BC =3a