Предмет: Алгебра,
автор: Аноним
Решите задание......
Приложения:
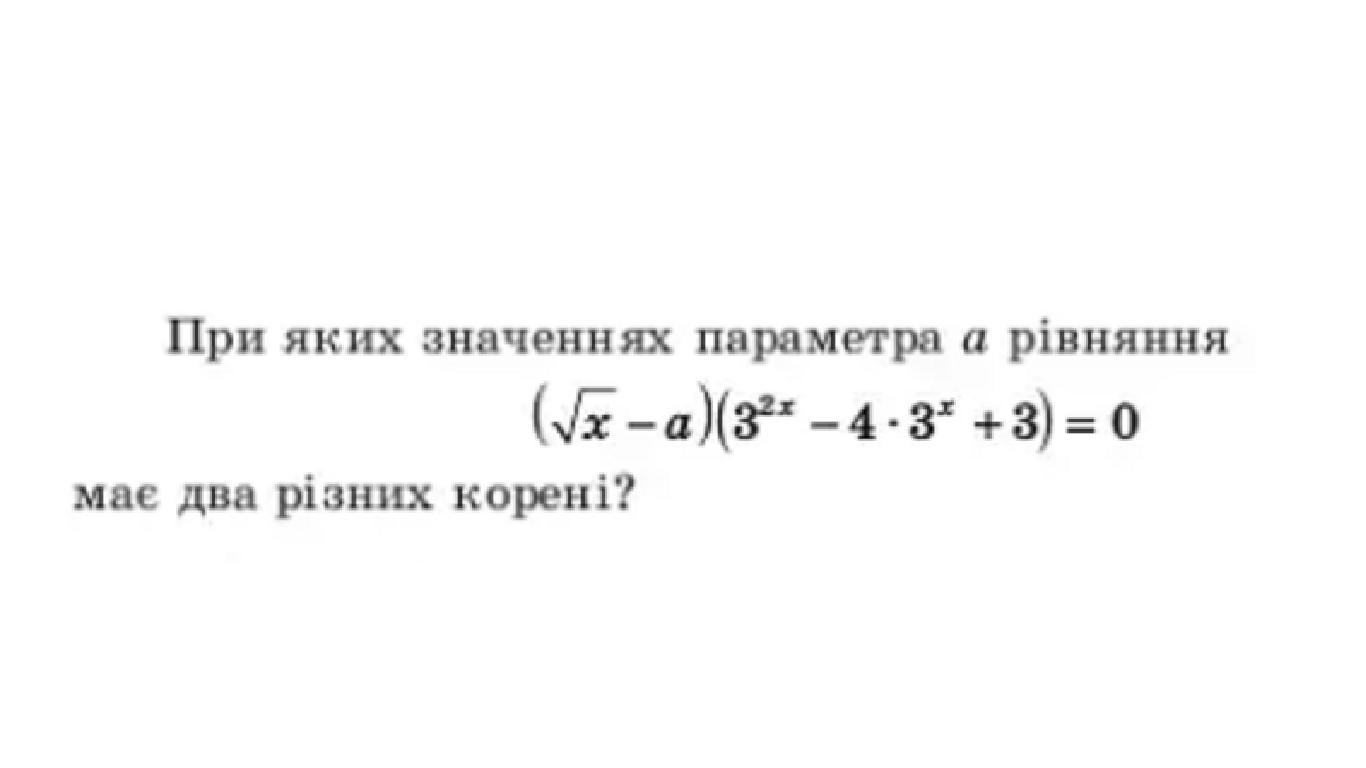
Ответы
Автор ответа:
1
, ОДЗ : x>=0
-----
Решим второе уравнение, делаем замену 3^x = t
Обратная замена :
-----
Заметим, что наше под уравнение уже имеет два корня, значит, чтобы все наше уравнение имело два корня, первое уравнение не должно иметь корней, или чтобы его корни совпади уже с решенныv :
1. Не имеет корней :
a < 0, т.к √x >= 0
2. Корень 1 совпадает :
√1 = a
a = 1
3. Корень 0 совпадает :
√0 = a
a = 0
Ответ : при а ∈ (-∞ ; 0] U {1}
Похожие вопросы
Предмет: Русский язык,
автор: vika2003olego
Предмет: Русский язык,
автор: айханым2
Предмет: Английский язык,
автор: Тася11111111111
Предмет: Литература,
автор: reginam800ey
Предмет: Геометрия,
автор: adasan131203