Предмет: Алгебра, автор: antonovm

Найдите сумму ряда :

Приложения:

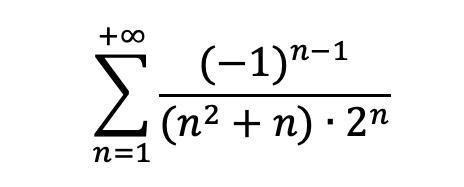
igorShap: Тут также предусмотрено школьное решение? Потому что, например, его можно свести к известному разложению в ряд Тейлора, но хочется найти более простое, если оно существует

antonovm: Нет , это задание для студентов

antonovm: Хотя в программу 11 класса школы 57 числовые ряды входят

igorShap: Понятно. Под школьным я имел в виду решение без рядов Тейлора, дифференцирования по параметру и.т.д., а чистыми заменами, группировками и преобразованиями членов ряда (естественно, обоснованными)

antonovm: Если поработать с бесконечно - убывающей геометрической прогрессией ( школьная тема ) , то можно , но обоснование возможности интегрирования ряда выходит за пределы школы ( если , конечно школа не математическая )

Ответы

Автор ответа: igorShap

Ответ:

$3\ln\dfrac{3}{2}-1$

Объяснение:

$\sum\limits_{n=1}^{+\infty}\dfrac{(-1)^{n-1}}{(n^2+n)\cdot 2^n}=\sum\limits_{n=1}^{+\infty}(-1)^{n-1}\cdot \underbrace{\dfrac{1}{(n^2+n)\cdot 2^n}}_{a_n}=(*)$

$a_n>0;\; \lim\limits_{n\to\infty}\sqrt[n]{a_n}=\dfrac{1}{2}<1$ , а значит, по радикальному признаку Коши, исходный ряд сходится абсолютно.

$a_n=\dfrac{1}{n(n+1)}\cdot \dfrac{1}{2^n}=\left(\dfrac{1}{n} -\dfrac{1}{n+1}\right)\cdot \dfrac{1}{2^n}$

$(*)=\sum\limits_{n=1}^{+\infty}(-1)^{n-1}\cdot\left(\dfrac{1}{n} -\dfrac{1}{n+1}\right)\cdot \dfrac{1}{2^n}\overset{[*]}{=} \sum\limits_{n=1}^{+\infty}\dfrac{1}{n} \cdot \dfrac{(-1)^{n-1}}{2^n}-\sum\limits_{n=1}^{+\infty}\dfrac{1}{n+1}\cdot \dfrac{(-1)^{n-1}}{2^n}=\\ =\sum\limits_{n=1}^{+\infty}\dfrac{1}{n} \cdot \dfrac{(-1)^{n-1}}{2^n}+\sum\limits_{n=0}^{+\infty}\dfrac{1}{n+1}\cdot \dfrac{(-1)^{n}}{2^n}-1=$

$=\sum\limits_{n=1}^{+\infty}\dfrac{1}{n} \cdot \dfrac{(-1)^{n-1}}{2^n}+\sum\limits_{k=1}^{+\infty}\dfrac{1}{k}\cdot \dfrac{(-1)^{k-1}}{2^{k-1}}-1=\\ =\sum\limits_{n=1}^{+\infty}\dfrac{1}{n} \cdot \dfrac{(-1)^{n-1}}{2^{n}}+2\sum\limits_{k=1}^{+\infty}\dfrac{1}{k}\cdot \dfrac{(-1)^{k-1}}{2^{k}}-1=3\sum\limits_{n=1}^{+\infty}\dfrac{1}{n} \cdot \dfrac{(-1)^{n-1}}{2^{n}}-1=\\ =3\sum\limits_{n=1}^{+\infty}\dfrac{(-1)^{n-1}\cdot (1/2)^{n}}{n} -1=(**)$

Используя известное разложение

$\sum\limits_{n=1}^{+\infty}\dfrac{(-1)^{n-1}\cdot x^{n}}{n}=\ln(x+1),|x|<1$ , получим

$(**)=3\ln\left(\dfrac{1}{2}+1\right)-1=3\ln\dfrac{3}{2}-1$

___________________________

Переход [*] справедлив, так как $\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{1}{n\cdot 2^n}}=\dfrac{1}{2}<1$ , то есть, по радикальному признаку Коши, каждый из рядов-слагаемых сходится абсолютно

igorShap: Еще была идея заменить 2 на параметр a, и затем 2 раза продифференцировать. Как раз в знаменателе n и n+1 уйдут

igorShap: -2, конечно

igorShap: Но, скорее всего, лучше там не вышло бы

antonovm: Спасибо , всё как всегда классно и хорошо , что в начале доказали сходимость , идея у меня была другой и я на неё намекал - просто проинтегрировать логарифмический ряд и подставить x = 1/2 , я думал , что произведение n(n+1) подскажет этот путь

antonovm: Вот это и есть " школьный путь " : 2 раза проинтегрировать сумму бесконечной геометрической прогрессии

antonovm: бесконечно - убывающей

igorShap: А. Я интегрирование не считал "школьным" методом. Но да, там хорошо выйдет, и значительно лучше, чем при дифференцировании. Спасибо

Автор ответа: Аноним

$\displaystyle \sum^{\infty}_{n=1}\frac{(-1)^{n-1}}{(n^2+n)2^n}=\sum^{\infty}_{n=1}\frac{(-1)^{n-1}}{n\cdot 2^n}-\sum^{\infty}_{n=1}\frac{(-1)^{n-1}}{(n+1)\cdot 2^n}$

Используем ряд Маклорена натурального логарифма

$\ln(1+x)=\displaystyle\sum^\infty_{n=1}\frac{(-1)^{n-1}x^n}{n}$

Проинтегрируем обе части равенства

$\displaystyle \int \ln(1+x)dx=\sum^{\infty}_{n=1}\int \frac{(-1)^{n-1}x^n}{n}$

$\displaystyle \int \ln(1+x)dx=\left\{\begin{array}{ccc}u=\ln(1+x);~~ du=\dfrac{dx}{1+x}\\ \\ dv=dx;~~~v=x\end{array}\right\}=x\ln(1+x)-\\\\ \int\frac{x}{1+x}dx=x\ln(1+x)-\int\left(1-\frac{1}{1+x}\right)dx=x\ln(1+x)-x+\ln(1+x)+C=\\ \\ =(x+1)\ln(1+x)-x+C$

Следовательно, $\displaystyle (x+1)\ln(1+x)-x=\sum^{\infty}_{n=1}\frac{(-1)^{n-1}x^{n+1}}{n^2+n}$ , разделив на х

$\displaystyle \frac{x+1}{x}\ln(1+x)-1=\sum^{\infty}_{n=1}\frac{(-1)^{n-1}x^n}{n^2+n}$

При x = 1/2 получаем $\displaystyle \sum^{\infty}_{n=1}\frac{(-1)^{n-1}}{(n^2+n)\cdot 2^n}=\frac{\frac{1}{2}+1}{\frac{1}{2}}\ln\left(1+\frac{1}{2}\right)-1=3\ln\frac{3}{2}-1=\ln\frac{27}{8}-1$