Question

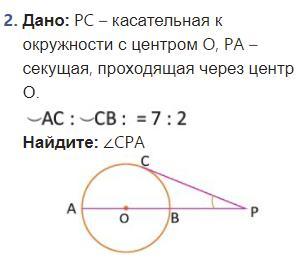
Дано: PC – касательная к окружности с центром O, PA – секущая, проходящая через центр О. AC:CB=7:2

Помогите пожалуйста решить задачу. Первый правильный ответ сразу отмечу лучшим.

Answer 1

дуга АСВ = 180°

дуга АСВ = 180°тогда 7х+2х= 180°

9х=180°

х=20°

дуга АС = 140°

дуга СВ = 40°

угол СРА = 1/2 (дугаАС-дугаСВ)= 1/2 (140°-40°)

= 50°

Ответ: 50°

Answer 2

Угол между касательной и секущей равен 1/2*(∪АС-∪СВ).

∪АС:∪СВ=7:2 ⇒ ∪АС=7/2*∪СВ

∪АС+∪СВ=180° ⇒ 7/2*∪СВ+∪СВ=180°  ⇒9/2*∪СВ=180° ⇒∪СВ=40°⇒∪АС=180°-40°=140°

∠СРА=1/2*(140°-40°)=50°