Предмет: Математика,
автор: wasska79
Дано: ML - касательная к окружности с центром O, LN:NK:KL=3:4:5 MK - секущая. Найдите: угол LMK
Ход решения непонятен. Данные на картинке. Заранее спасибо за ответы
Приложения:
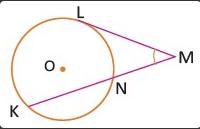
wasska79:
cорян, исправил
Ответы
Автор ответа:
1
Ответ:
∠LMK=30°
Пошаговое объяснение:
Найдём градусную меру дуг KL, LN и NK и обозначим их соотношение 3х, 4х, 5х, и зная, что градусная мера всей окружности равна 360°, составим уравнение:
3х+4х+5х=360
12х=360
х=360÷12
х=30°
Тогда ∪LN=3×30=90°
∪NK=4×30=120°
∪KL=5×30=150°
Угол, образуемый касательной и секущей равен половине разности величин дуг, заключённых между сторонами этого угла:
∠LMK=(∪KL–∪LN)/2=(150–90)/2=60÷2=30°
Похожие вопросы
Предмет: Русский язык,
автор: ттымтвл
Предмет: Английский язык,
автор: Ankasovogirova
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: лаганитТВ
Предмет: Математика,
автор: Dgvxfgbdhncs