Question

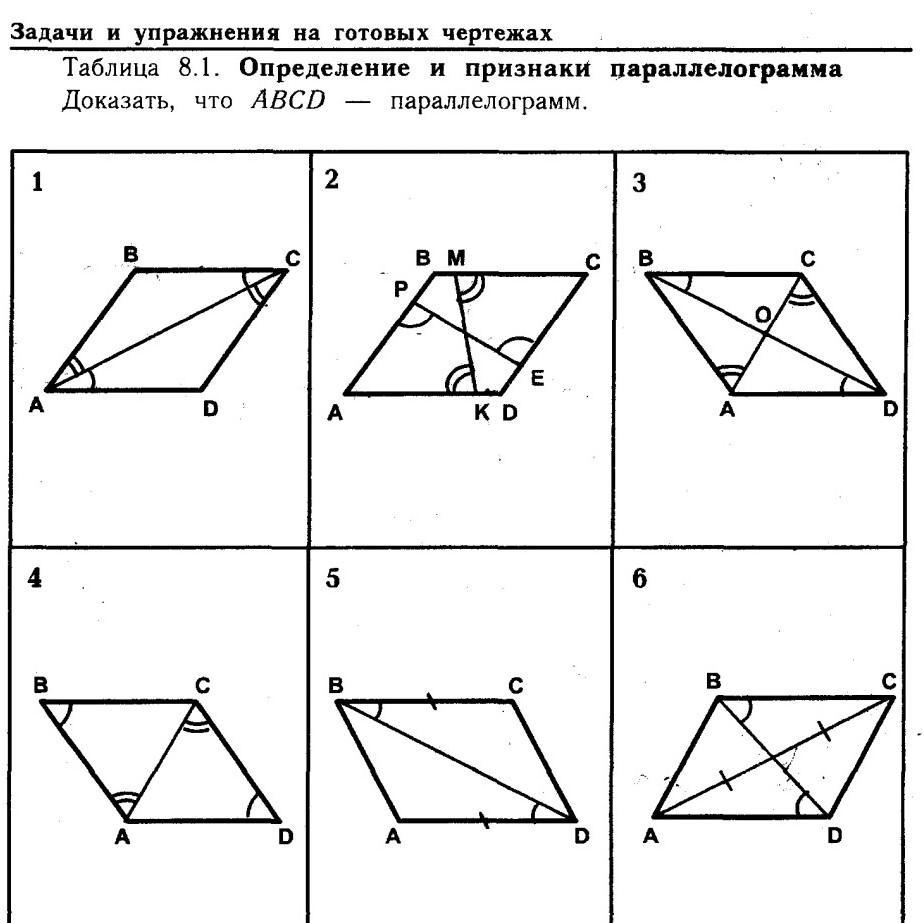
Ребят пжж помогите (с пояснениями) пж прошуу ​

Answer 1

Ответ:

Объяснение:

Определение:

1. Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.

Признаки:

2. Две противоположные стороны равны и параллельны.

3. Противоположные стороны попарно равны.

4. Диагонали точкой пересечения делятся пополам.

1. Рассмотрим ΔABC и ΔACD.

AC-общая.

∠1=∠4 (условие)

∠2=∠3 (условие)

⇒ ΔABC = ΔACD (2 признак)

⇒ AB=CD; BC=AD (соответственные элементы)

АВСD - параллелограмм (признак, п.3)

2. ∠1=∠4 (условие) - накрест лежащие при AB и CD и секущей РЕ.

⇒ AB║CD

∠2=∠3 (условие) - накрест лежащие при ВС и AD и секущей МК.

⇒ ВС║AD

AВСD - параллелограмм (определение, п.1)

3. ∠1=∠2 (условие) - накрест лежащие при ВС и AD и секущей BD.

⇒ ВС║AD

∠3=∠4 (условие) -  накрест лежащие при AB и CD и секущей АС.

⇒ AB║CD

AВСD - параллелограмм (определение, п.1)

4. Рассмотрим ΔАВС и ΔACD.

∠1=∠2 (условие)

∠3=∠4 (условие)

∠ВСА=180°-(∠1+∠3) (сумма углов Δ)

∠CAD=180°-(∠2+∠4) (сумма углов Δ)

⇒ ∠ВСА=∠CAD

АС - общая

⇒ ΔАВС = ΔACD (2 признак)

⇒ ВС=AD; AB=CD (соответственные элементы)

АВСD - параллелограмм (признак, п.3)

5. ∠1=∠2 (условие) - накрест лежащие при ВС и AD и секущей BD.

⇒ ВС║AD

ВС=AD

АВСD - параллелограмм (признак, п.2)

6. Рассмотрим ΔВОС и ΔAOD.

∠1=∠2 (условие)

∠ВОС=∠AOD (вертикальные)

∠ВСО=180°-(∠1+∠ВОС)

∠OAD=180°-(∠2+∠AOD)

⇒ ∠ВСО=∠OAD

АО=ОС (условие)

⇒ ΔВОС = ΔAOD (2 признак)

⇒BO=OD (соответственные элементы)

АВСD - параллелограмм (признак, п.4)