Предмет: Алгебра,
автор: antonovm
Решите уравнение : //////////////////////////
Приложения:
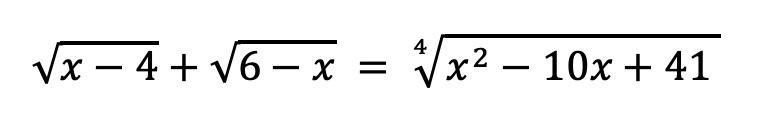
amanda2sempl:
возводим в квадрат и делаем замену: - (х² - 10х + 24) = t; 2 + 2√t = (17 - t)^0,5 или типа того получается
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Введем замену :
1) Согласно неравенству между средним арифметическим и средним квадратичным
2)
Но тогда уравнение равносильно системе
Из 2ого уравнения системы получаем возведением в 4 степень
Возвращаясь к исходной переменной, получим
Подставим в условие:
- верно
Замечательно !
Похожие вопросы
Предмет: Русский язык,
автор: Dasha2016and2019
Предмет: Русский язык,
автор: 111287
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Hello123456789098
Предмет: Окружающий мир,
автор: Evochcaзвезда