Предмет: Алгебра,
автор: Демоныдомашки
Найти наименьшее и наибольшее значение функции.
Приложения:
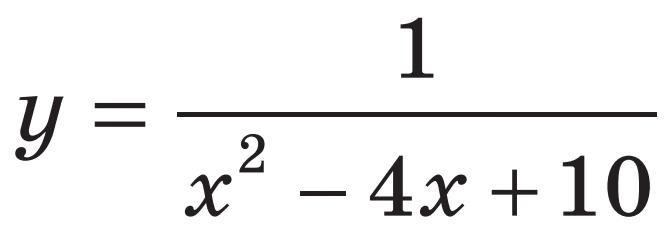
tamarabernukho:
Наиб значение при наименьшем знаменателе:y=1/((x^2-4x+4)+6)=1/((x-2)^2+6)>=1/(0+6)=1/6 при х=2
Ответы
Автор ответа:
1
Ответ:
Объяснение:
первая производная
приравняем ее к нулю (знаменатель ≠ 0)
-2x+4 = 0 ⇒ x = 2 это точка экстремума и она только одна
y(2) = 1/6
теперь надо определить, это минимум или максимум
для этого возьмем вторую производную
y''(2) = -1/18 < 0, значит точка х=2 - это точка максимума
ответ
наибольшее значение функции у(2) = 1/6
можно же не брать вторую производуную
а узнать знаки производной слева и справа от нуля
можно. но по теории все-таки вторая производная -)))
Похожие вопросы
Предмет: Другие предметы,
автор: Гарик111111
Предмет: Английский язык,
автор: a9syamsvetyDiana
Предмет: Русский язык,
автор: весна16
Предмет: Математика,
автор: Kim888