Question

В правильной четырехугольной призме диагональ основания относится к диагонали боковой грани как 2÷3. Найдите объем этой призмы, если площадь основания равна 14 кв.дм.​

Answer 1

Ответ:

98дм³

Пошаговое объяснение:

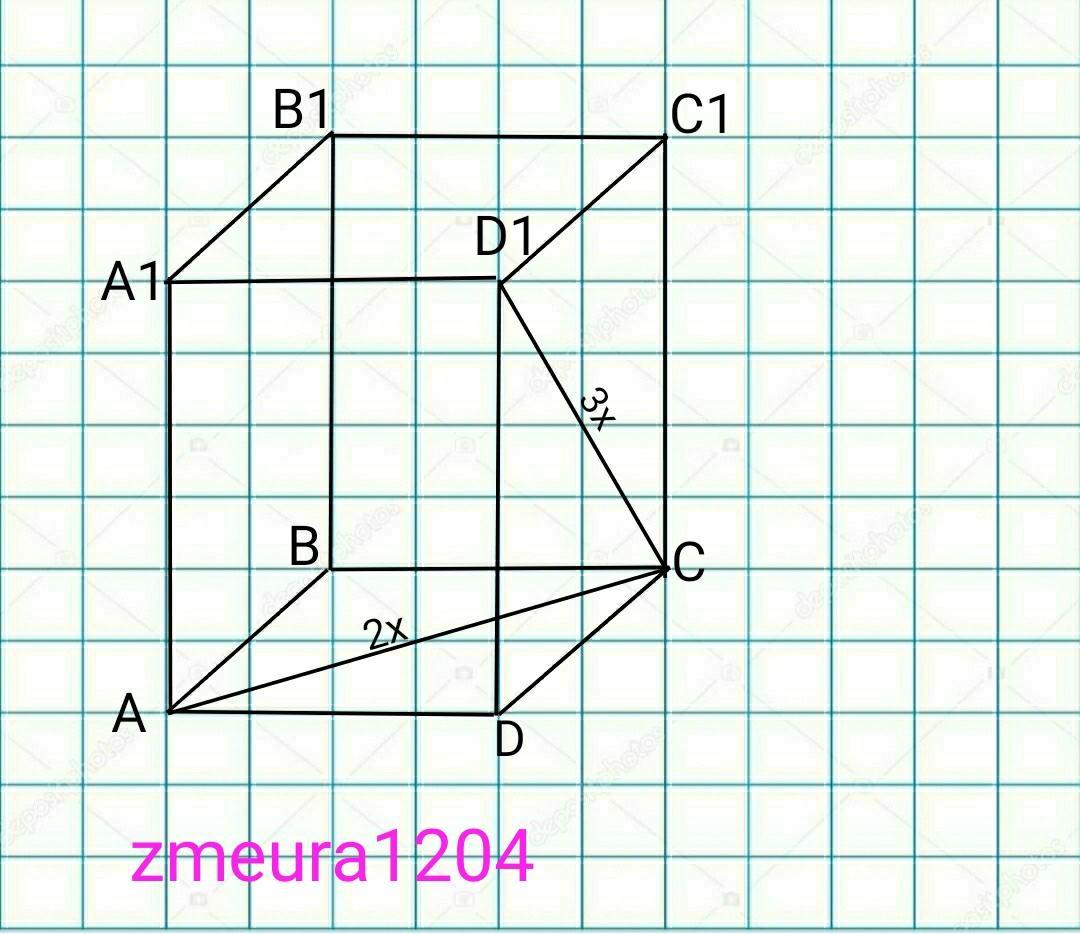
S(ABCD)=14дм²

S(ABCD)=AB² → AB=√S(ABCD)=√14 дм сторона квадрата основания.

Теорема Пифагора

АС=√(АВ²+ВС²)=√((√14)²+(√14)²)=√(14+14)=

=√28=2√7 дм.

АС:D1C=2:3 по условию

АС=2х;. D1C=3x

2x=2√7

x=2√7/2

x=2.

D1C=3x=3√7 дм

Теорема Пифагора

DD1=√(D1C-DC)=√((3√7)²-(√14)²)=√(63-14)=

=√49=7дм

V=S(ABCD)*DD1=14*7=98дм³