Предмет: Математика,
автор: pomidorkasvezhaya
Какие действия можно заменить на более простые? Или решите просто более коротким способом, если знаете как. Я не придумала ничего лучше. Нужно сделать решение минимально загруженным.
жалобу отправлю, если не в тему писать будете
Приложения:

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
..
Приложения:
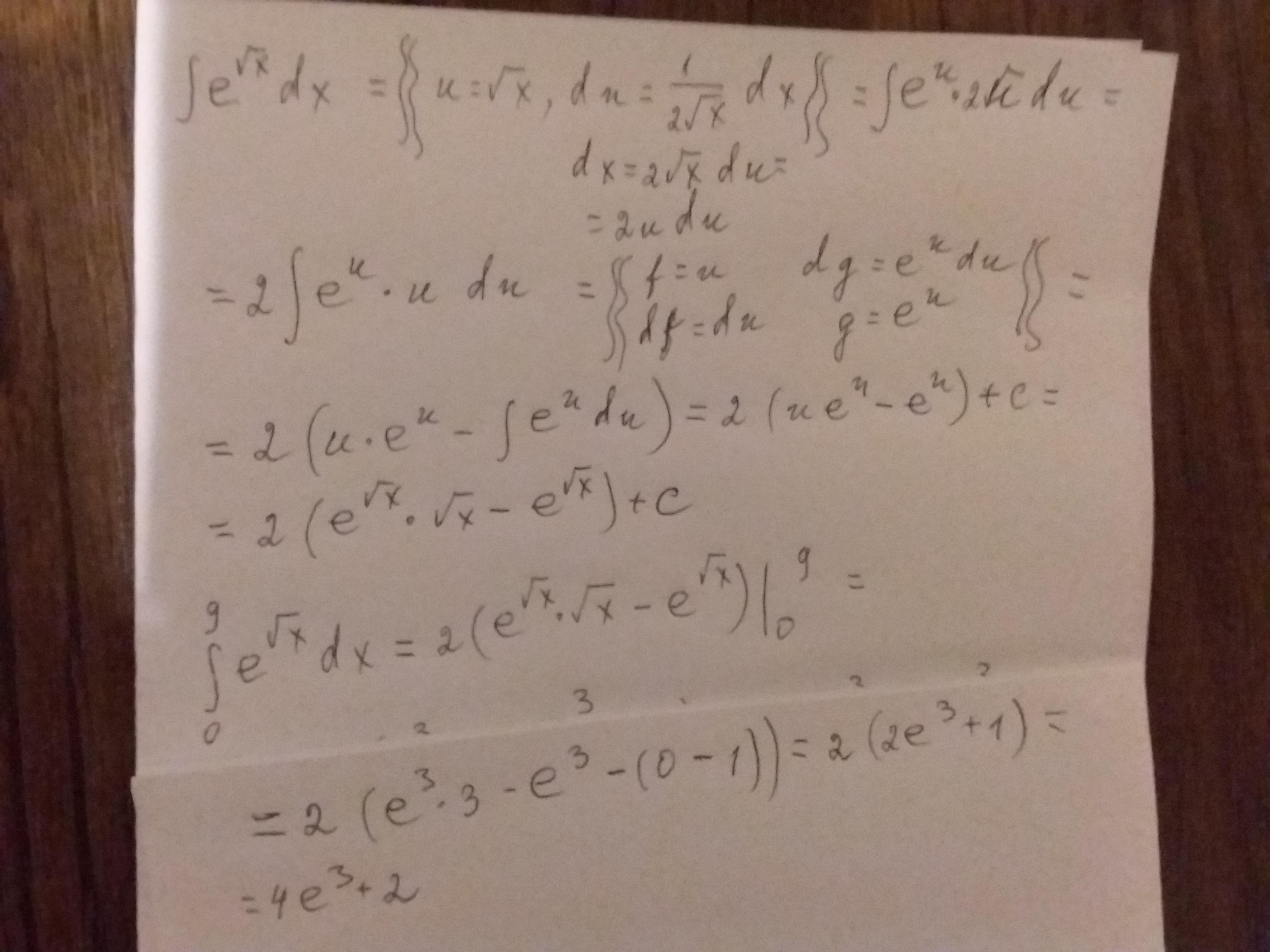
pomidorkasvezhaya:
спасибо
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: mrfeikfeikovich
Предмет: Русский язык,
автор: каприза2
Предмет: Русский язык,
автор: hant79
Предмет: Английский язык,
автор: nleonid56