Question

Найдите все значения параметра а, про каждом из которых неравенство имеет равно два решения. Укажите эти решения для каждого из найденных значений параметра (7^(x)-49)((0,5)^(-x)-8)((0,2)^(-x)-125^(a))(3^x-3*27^a)<=0 Хотя бы примерно скажите как решать пожалуйста!!!!!!!!!!!

Answer 1

Ответ:

(см. объяснение)

Пошаговое объяснение:

$(7^x-49)((0.5)^{-x}-8)((0.2)^{-x}-125^a)(3^x-3\cdot27^a)\le0$

Приравняем к нулю каждую скобку и получим:

• $x=3a$
• $x=3a+1$
• $x=2$
• $x=3$

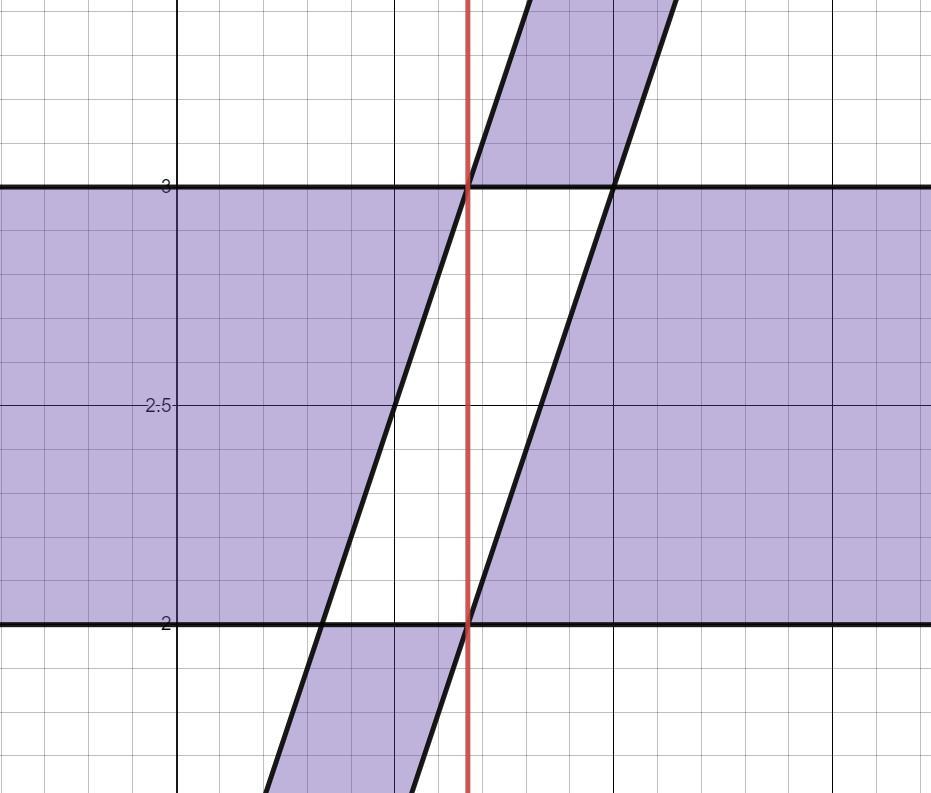
В координатах $(a;\;x)$ это прямые, которые можно построить. Видим, что координатная плоскость оказалась разбита на области. Берем произвольную точку в любой из них и подставляем в неравенство. Если оно верно, то такую область закрасим, иначе оставим как есть. Затем либо продолжаем брать точку из каждой области и считать, либо упрощаем: для областей идущих через точку стиль сохраним, иначе используем противоположный. Получим график решений неравенства. На нем отметим все удовлетворяющие условию случаи.

Итоговый результат:

(см. прикрепленный файл)

Убеждаемся, что изображенный нами случай достоверен, а не получен из-за искажений при построении графика.

$\left\{\begin{array}{c}x=3\\x=3a+1\end{array}\right,\;=>\;a=\dfrac{2}{3}\\\\\\\left\{\begin{array}{c}x=2\\x=3a\end{array}\right,\;=>\;a=\dfrac{2}{3}$

Итого при $a=\dfrac{2}{3}$ исходное неравенство имеет ровно два решения: $x=2$ и $x=3$.

Задание выполнено!