Предмет: Алгебра,
автор: savatinao
Помогите пожалуйста. При каком значении а уравнение (a/(x^2-4x+7))-4x=3-x^2 имеет три решения? Фото уравнения прилагаю
Приложения:
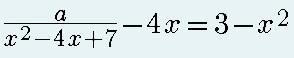
Ответы
Автор ответа:
0
Ответ:
(см. объяснение)
Объяснение:
Выполним преобразования:
Сделаем замену вида .
Тогда уравнение примет вид:
Вернемся к записи .
Заметим, что:
- Если
, получим два
.
- Если
, то один.
- Если
, корней не будет.
Тогда, чтобы исходное уравнение имело три решения, нужно чтобы корнями уравнения были
и любое
.
Опираясь на этот вывод, выполним необходимые вычисления:
При :
Итого при исходное уравнение имеет ровно три различных корня.
Задание выполнено!
Похожие вопросы
Предмет: Русский язык,
автор: 58000Liliya
Предмет: Русский язык,
автор: Lider552
Предмет: Русский язык,
автор: ЛаугаКаваи
Предмет: Английский язык,
автор: nastia5078