Question

Момент волнения поверхности воды может быть смоделирован с помощью графика функции f(x)=sin4x .Сколько точек максимума у волн (графика функции) может быть на отрезке [0;2п]?

​

Answer 1

Для нахождения точек максимума можно найти нули производной функции от функции момента волнения.

f'(x)=cos(4x)*[4x]'=4cos(4x).

4cos(4x)=0.

cos(4x)=0.

4x=Π/2+Πk, k-целое.

x=Π/8+2Πk/8.

На данном отрезке перебиру значения x чтобы найти экстремумы.

x=Π/8 k=0

x=3Π/8 k=1

x=5Π/8 k=2

x=7Π/8 k=3

x=9Π/8 k=4

x=11Π/8 k=5

x=13Π/8 k=6

x=15Π/8 k=7

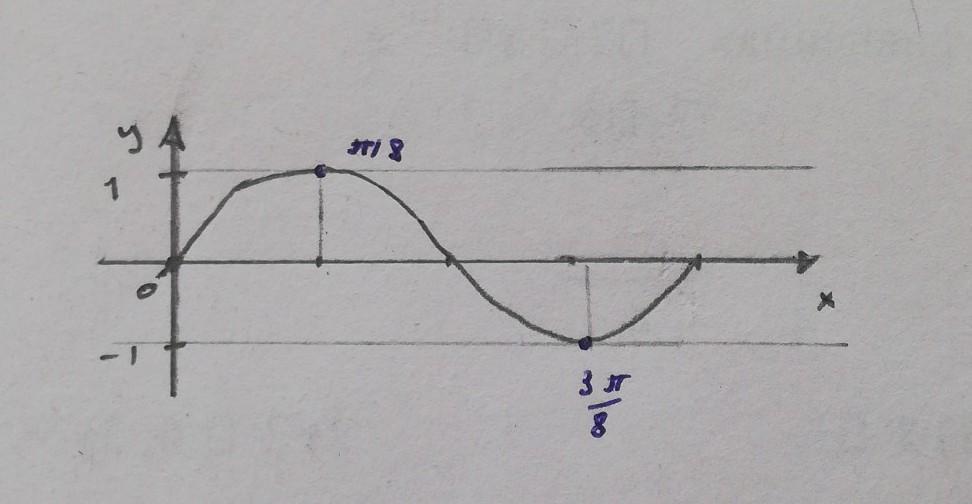
Схематически изображу часть графика функции y=sin(4x), определю, какие из точек экстремума точки максимума. Максимумы и минимумы чередуются у синусоиды, т.е. подходят

x=Π/8, x=5Π/8, x=9Π/8, x=13Π/8.

Итого 4 точки максимума.