Предмет: Алгебра,
автор: benlinus130
Необходимо найти среднее арифметическое корней уравнения.
(вероятно решается через замену, но какую – не ясно)
Приложения:
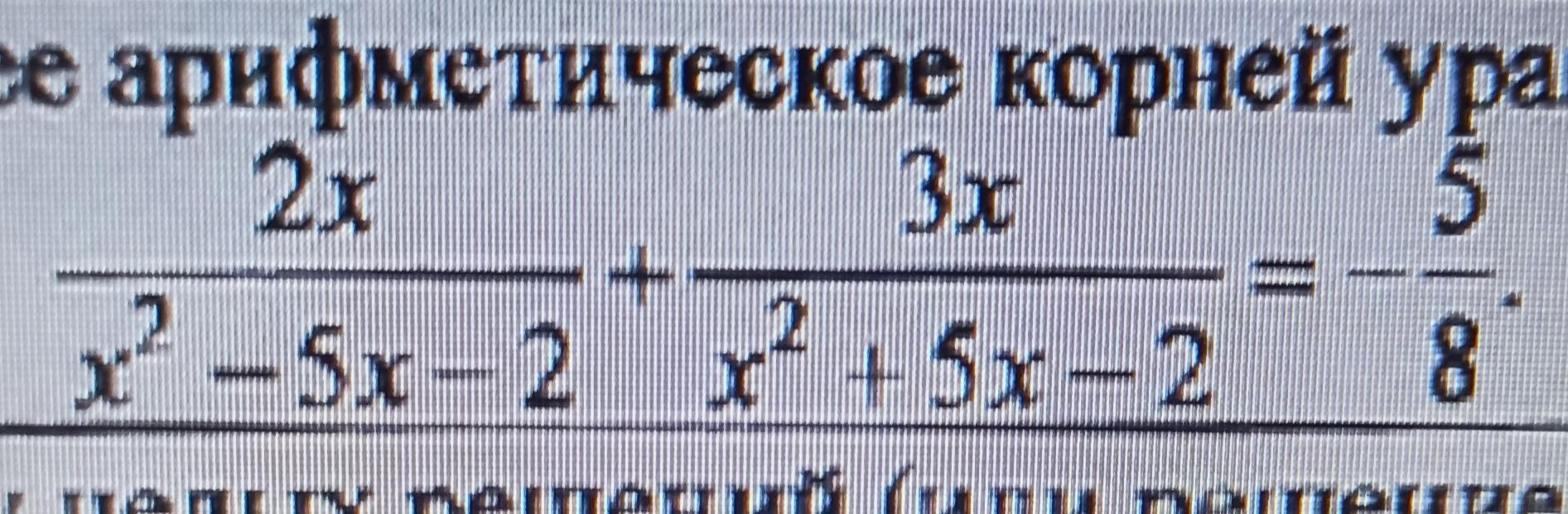
Ответы
Автор ответа:
1
x^2-5x-2=a
x^2+5x-2=b
Тогда
b-a=10x
x=(b-a)/10
Подставляя
(b-a)/(5a) + (3*(b-a))/(10b) = -5/8
(b-a)*(1/(5a)+3/(10b)) = -5/8
(b-a)*(2b+3a)/(10ab) + 5/8 = 0
8(b-a)(2b+3a)+50ab = 0
8(8b^2+ab-3a^2)+50ab = 0
64b^2+8ab-24a^2+50ab = 0
64b^2+58ab-24a^2=0
2*(8b-3a)(4a+b)=0
1) 8b=3a
2) b=-4a
1) 8x^2+40x-16=3(x^2-5x-2)
2) x^2+5x-2=-4*(x^2-5x-2)
1) 5x^2+55x-10=0
2) 5x^2-15x-10=0
1) x^2+11x-2=0
2) x^2-3x-2=0
По теореме Виета
x1+x2+x3+x4/4 = (-11+3)/4 = -8/4 = -2
antonovm:
У вас ошибка после сокращения на 5 второго уравнения : x^2-3x-2=0
Спасибо, только последнее уравнение с минусом (см. до сокращения) и среднее арифметическое (-11+3)/4=-8/4=-2
Автор ответа:
2
Ответ:
-2
Объяснение:
Приложения:

Делил на х числитель и знаменатель каждой дроби ( не обе части уравнения )
Михаил, можете в ЛС написать мне? Хочу узнать об материалах.
Похожие вопросы
Предмет: Русский язык,
автор: Линк255
Предмет: Другие предметы,
автор: GenusMandarinka
Предмет: Беларуская мова,
автор: Томасянчик
Предмет: Алгебра,
автор: Лёша11111111239399
Предмет: Русский язык,
автор: ЕлизаветаДобрая