Предмет: Алгебра,
автор: antonovm
Найдите наибольшее значение функции :
Приложения:
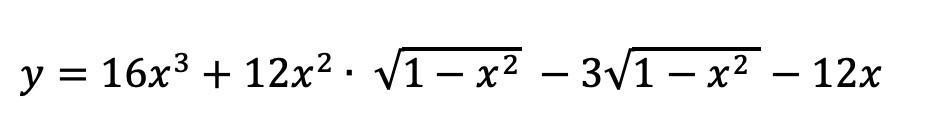
Ответы
Автор ответа:
3
Можно переформулировать задачу, если заменить
x=sina
Тогда подставив , функция принимает вид
y=sina*(16*sin^2a-12)+(12*sin^2a-3)*cosa = 16sin^3a-12sina+9cosa-12cos^3a = -(4sin(3a)+3cos(3a))
Тогда по неравенству Коши-Буняковского
(4sin(3a)+3cos(3a)) <= V((4^2+3^2)*(cos^2(3a)+sin^2(3a)) = 5
То есть y=5
antonovm:
1) Если вы делаете замену надо указать как изменяется новая переменная , вы же заменяете косинус на корень со знаком + , то есть считаете его положительным , значит а не может принимать все значения
2) в конце решения у вас оценка , оценка верная , но должно быть равенство , то есть надо указать х , при котором она достигается
Просто написать, что a=arcsin x
Да или указать , что а входит в отрезок [ -pi/2 ; pi/2] , тогда не надо будет везде писать + - как пришлось сделать автору второго решения
Автор ответа:
1
Ответ:
5
Объяснение:
Ограничения:
1-х²≥0 ⇔ х²≤1 ⇔ |x|≤1 ⇔ x ∈ [-1;1]
Исходя из такого ограничения, можно сделать замену
x=sint, так как -1≤sint≤1
y=±5sin(3t+γ)
Так как -1≤sin(3t+γ)≤1, то
-5≤±5sin(3t+γ)≤5
Похожие вопросы
Предмет: Английский язык,
автор: weermiopcomgha4
Предмет: Українська мова,
автор: Doc857
Предмет: Другие предметы,
автор: davidav12166
Предмет: Русский язык,
автор: lotoc1973
Предмет: Психология,
автор: Аноним