Question

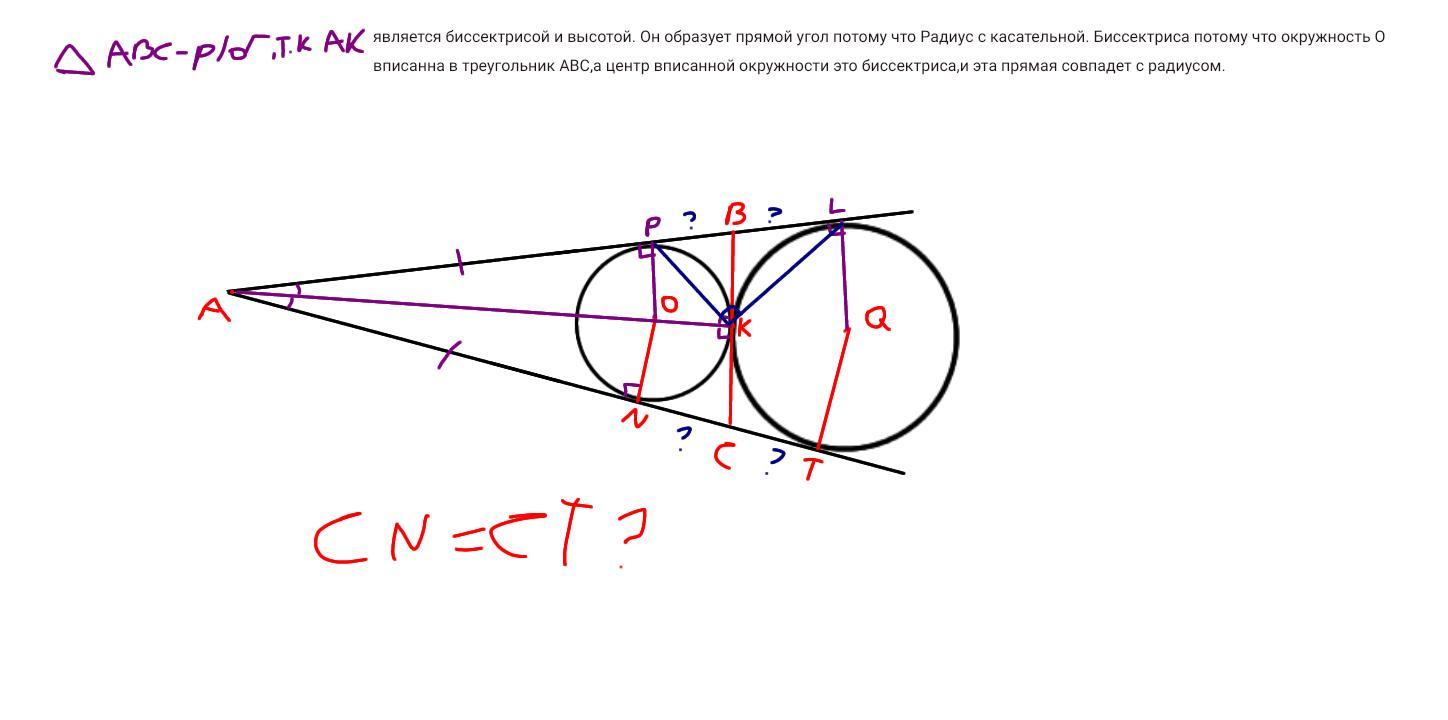
Задача : Даны две окружности ,они касаются внешним образом. Путь точка внешнего касания окружностей это точка K. И проведенны две касательные из одной точки , которые касаются к каждой окружности . Мы сделаем прямую через точку K. И были проведены радиусы . Докажите что CN=CT. Смотрите рисунок и описание к задаче.

Докажите что CN=CT . Не пишите что по теореме о отрезках касательных. Я не вижу или не понимаю ,это теорема говорит то что AP=AN ,но я не вижу как она взаимодействонна с CT и CN. Зная это я смогу доказать что CT=CN=CK,по свойству медианы прямоугольного треугольника, проведённая из вершины прямого угла.Так как CK медиана проведённая из вершины прямого угла. Дело не в этом ,я не вижу что CN=CT. Не разумные пожалуйста не отвечайте на этот вопрос как , свойство отрезков касательной,без доказательства к рисунку,или есть ещё хуже что отвечают что нет условия и задача так себе. И удаляют вопрос .
Треугольник ABC равнобедренный . Так как в него вписанна окружность O,а центр этой окружности это точка пересечения биссектрис. AO биссектриса и если продолжить эту прямую,то она образует прямой угол,так как Радиус образует прямой угол между касательной . Если я ошибаюсь напишите. Отсюда следует что AB=AC. По свойству отрезков касательной AL=AT. Здесь надо сделать какие-то действия что доказывают что CN=CT. Я их не вижу. Можно написать что PB=NC и BL=CT. Серьезно докажите это. Если я думаю не правильно,или в моем описании есть ошибки, поправьте меня. Даже на рисунке ,не точном видно что они равны,но я не могу доказать это ... ... Только нормальные ответы,без непонятно или в пару слов.

Answer 1

1)   Рассмотрим  ΔONC и ΔOKC.

У них:  

    ∠ONC= ∠OKC=90°

     ON=OK=r (радиусы одной окружности)

    сторона OC-общая

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

Из равенства треугольников следует равенство соответственных сторон.

   ΔONC =  ΔOKC     =>   CN=KC

2) Рассмотрим  ΔQKC и ΔQTC  (рассуждаем аналогично)

У них

∠QKC= ∠QTC=90°  

ON=OK=R   (радиусы одной окружности)

QC-общая

ΔQKC =  ΔQTC    =>   КС=CT

3) Если CN=KC,  а KC = CT, то =>  CN=CT  Если каждая из двух данных сторон равна третьей, то эти стороны равны между собой (свойство транзитивности).

Доказано.