Предмет: Алгебра,
автор: yugolovin
Решить уравнение
![\frac{\left(\sqrt[3]{(1+x)^2}+\sqrt[3]{(1-x)^2}\right)^2}{\sqrt[3]{1+x}+\sqrt[3]{1-x}}=2 \frac{\left(\sqrt[3]{(1+x)^2}+\sqrt[3]{(1-x)^2}\right)^2}{\sqrt[3]{1+x}+\sqrt[3]{1-x}}=2](https://tex.z-dn.net/?f=%5Cfrac%7B%5Cleft%28%5Csqrt%5B3%5D%7B%281%2Bx%29%5E2%7D%2B%5Csqrt%5B3%5D%7B%281-x%29%5E2%7D%5Cright%29%5E2%7D%7B%5Csqrt%5B3%5D%7B1%2Bx%7D%2B%5Csqrt%5B3%5D%7B1-x%7D%7D%3D2)
Аноним:
привет
архиавирус
чо ты ответ ты знаешь ты ж умный
Yugolovin, спасибо большое за интересное уравнение
Ответы
Автор ответа:
6
Ответ: Прикрепляю снимки
PS. Знаменатель данной дроби не обращается в ноль, поскольку для этого должно выполниться: , откуда
(обе части возводим в куб, нечётную степень) ⇔
1 + х = - (1 - х) ⇒ х + 1 = х - 1, что невозможно ∀х∈R ⇒ ни при каких вещественных "икс" знаменатель дроби не равен нулю
Приложения:

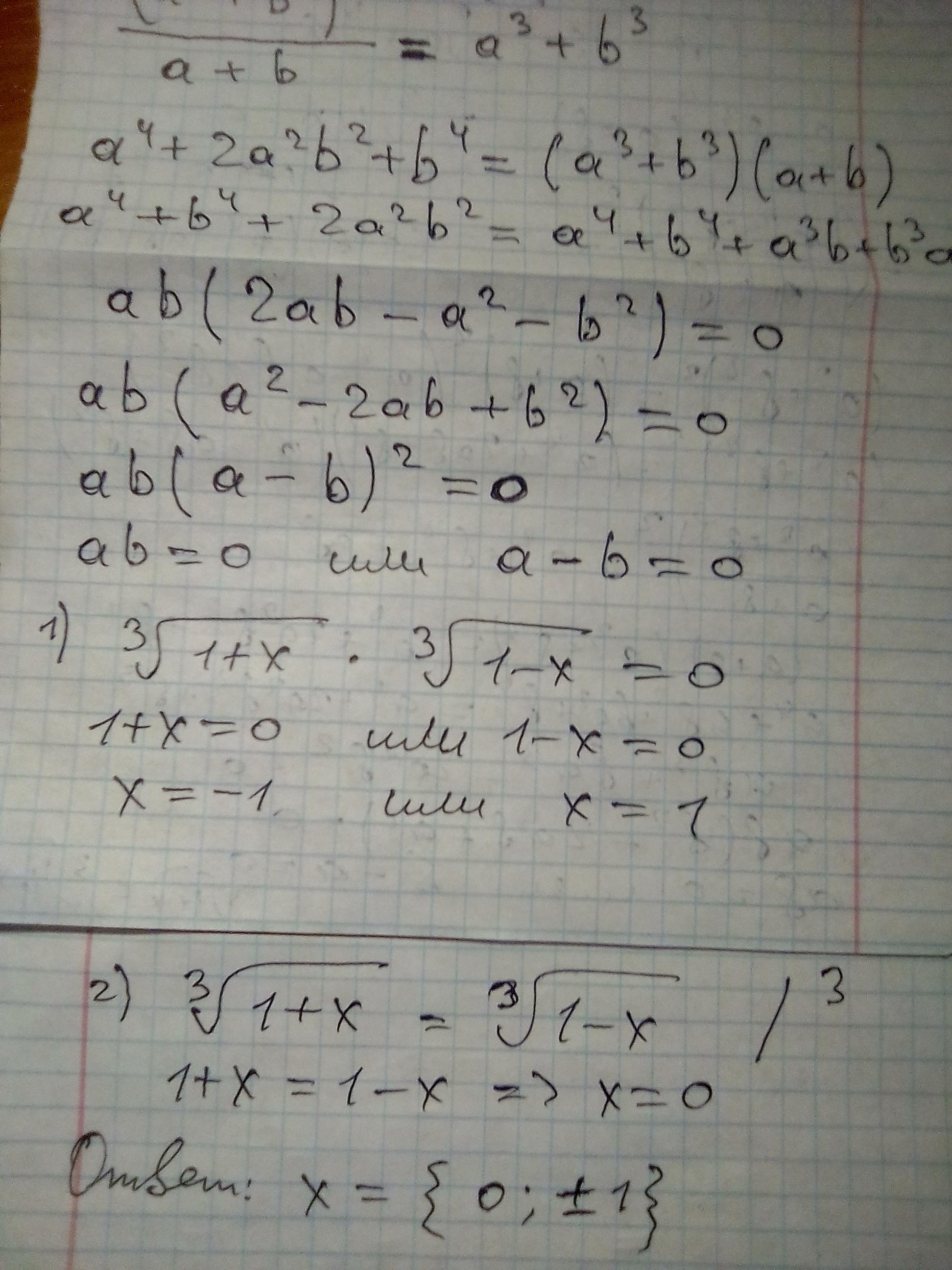
Скажите, все ли преобразования были равносильны ?
В четную степень вроде нигде не возводилось – пожалуй, все
дополнительно не возводилось; формулу сокращенного умножения, дело ясное, не обойти стороной
А знаменатель?
при ∀х∈R знаменатель не обращается в ноль, так как для этого должно выполняться: 1 + х = – 1 + х
А еще не поздно в основной текст это включить ?
Стоило после замены указать, что a не=-b. В данном примере посторонний корень не выскочил, но в другом может. В остальном все верно, я тоже таким способом решил.
Похожие вопросы
Предмет: Русский язык,
автор: Masha20071
Предмет: Английский язык,
автор: mariei
Предмет: Русский язык,
автор: ttastanbek
Предмет: Математика,
автор: znanija175
Предмет: Музыка,
автор: perevozkannp6m81f