Question

помогите срочно нужно
Геомоетрия

Answer 1

Ответ:

$OE=4\sqrt{3}$

Объяснение:

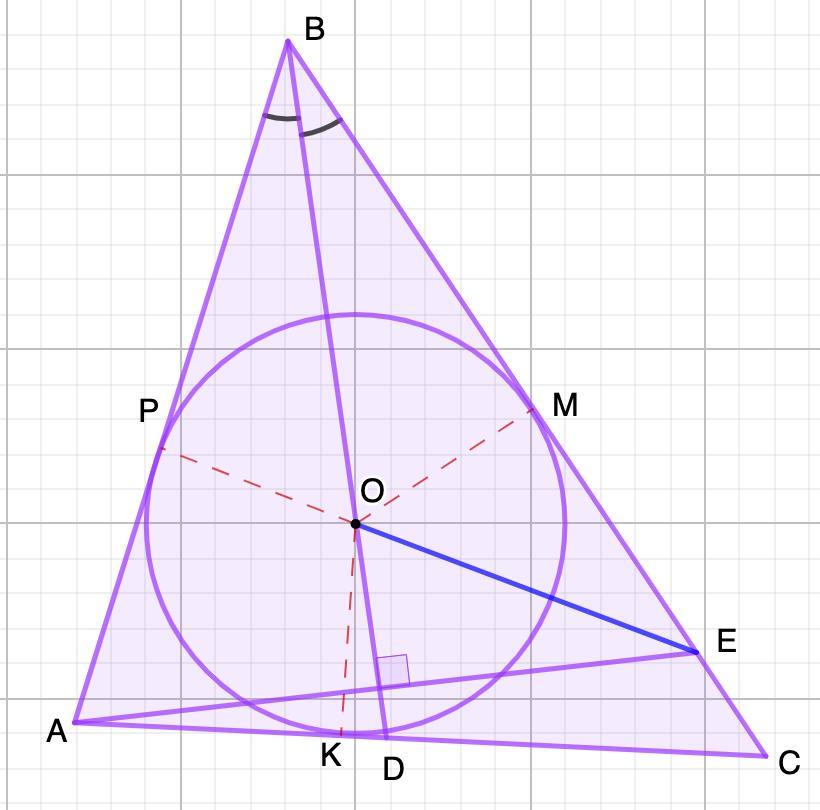
Дано: ΔАВС

BD - биссектриса; АЕ⊥BD;

Окр.Or;

AB=24; BC=36; AC=20.

Найти: ЕО.

Решение:

1. Найдем периметр ΔАВС:

$P=24+36+20=80$

2. AD=AP (отрезки касательных)

   DC=CM (отрезки касательных)

⇒AD+DC=AP+CM

или АС=AP+CM=20,

тогда AD+DC+AP+CM=40.

3. ВМ=ВР (отрезки касательных)

ВМ+ВР=80-40=40

⇒ВМ=ВР=40:2=20.

4. Рассмотрим ΔАВЕ.

ВD - биссектриса, высота ⇒ ΔАВЕ - равнобедренный

⇒АВ=ВЕ=24.

Отсюда

МЕ=ВЕ-ВМ=24-20=4

5. Найдем площадь ΔАВС по формуле Герона:

Полупериметр равен

$p=80:2=40\\S=\sqrt{40(40-24)(40-36)(40-20)}= 160\sqrt{2}$

6. Найдем радиус вписанной окружности:

$r=\frac{2S}{P}=\frac{2*160\sqrt{2} }{80}=4\sqrt{2}$

7. Рассмотрим ΔЕОМ - прямоугольный (радиус ⊥ касательной)

По теореме Пифагора:

$OE=\sqrt{ME^2+r^2}= \sqrt{16+32} =4\sqrt{3}$