Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить
Приложения:
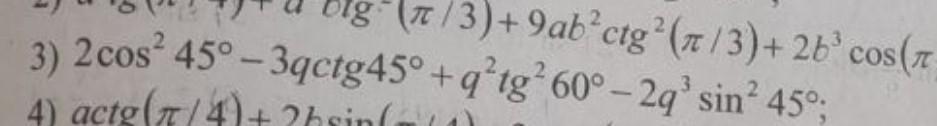
matilda17562:
как сформулировано задание? Что нужно сделать?
Ответы
Автор ответа:
0
Как я понял, это выражение нужно упростить. Поскольку
получаем
Если упростить, то Вы выполнили лишние действия. Результат должен быть в виде одночлена стандартного вида. А Вы выполнили разложение на множители
Я дал на выбор два варианта ответа - выбирайте, какой нравится больше. Кстати, в условии задачи ничего не сказано о том, то требуется,
Задание сформулировано в комментарии к заданию.
Интересно, если упрощаемое выражение привелось к виду x^9+C_9^1x^8+C_9^2x^7+...+C_9^8x+1, надо так оставлять, или все же лучше написать (x+1)^9?
Если "упростить", то только в виде многочлена стандартного вида.
Автор ответа:
0
Подставим:
(по формуле
)
Ответ:
Похожие вопросы
Предмет: Окружающий мир,
автор: зара25
Предмет: Окружающий мир,
автор: elzamag
Предмет: Русский язык,
автор: Эдик06
Предмет: Литература,
автор: Алиса20710
Предмет: Математика,
автор: Аноним