Предмет: Математика,
автор: greyyoume
Разложите на множители
Приложения:
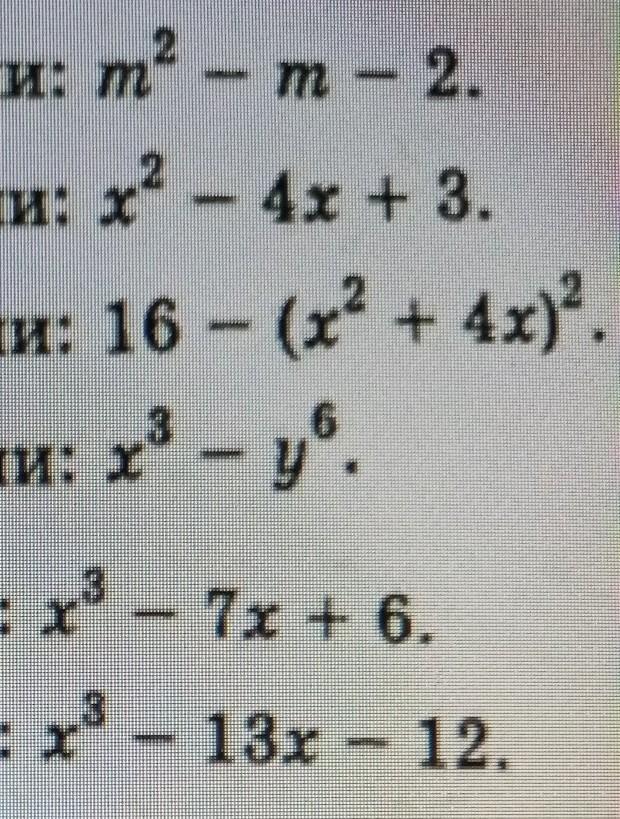
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
_______
Приложения:
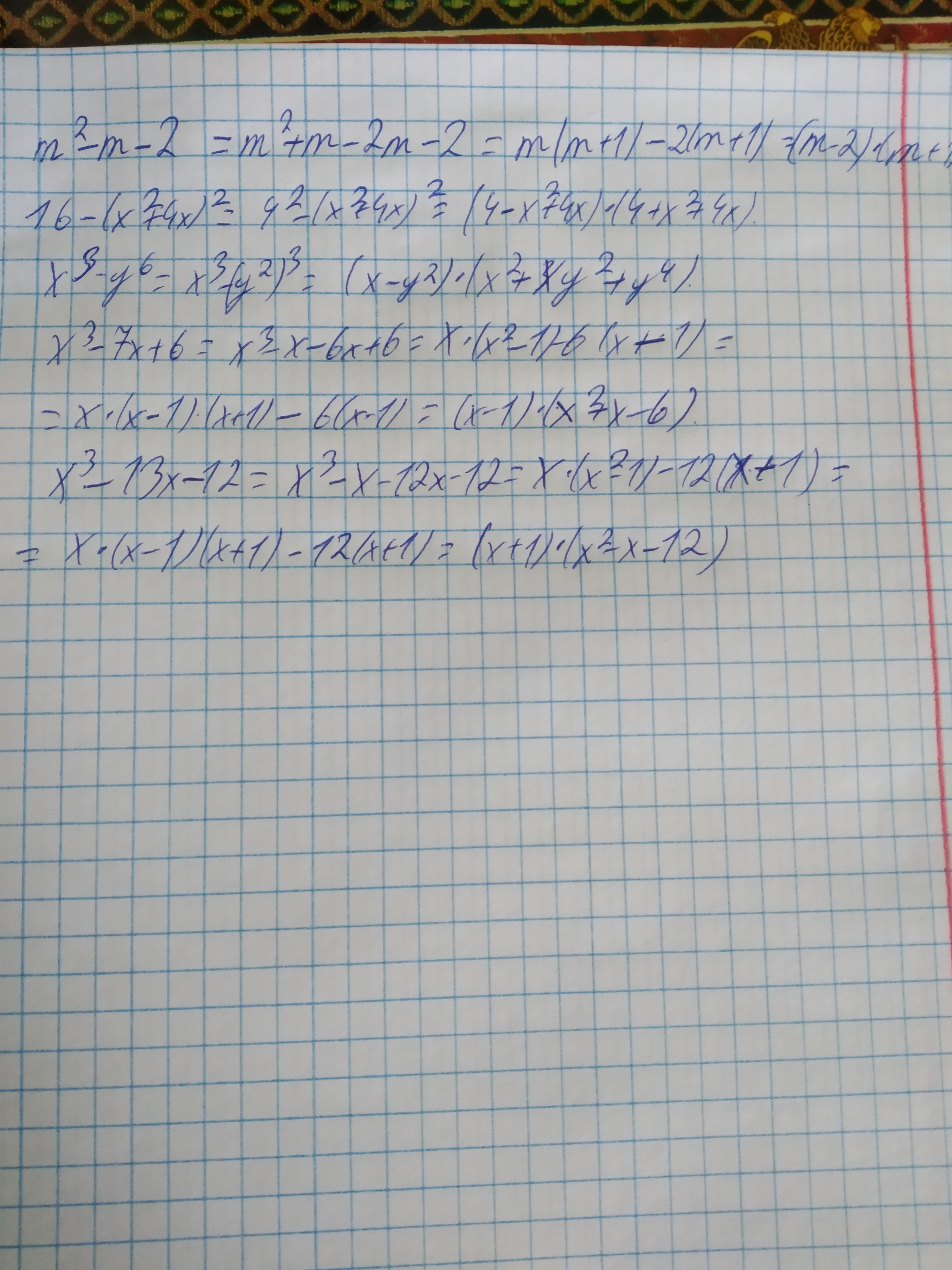
Автор ответа:
1
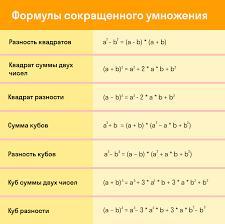
Ответ
Пошаговое объяснение:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: VeronikaNu
Предмет: Русский язык,
автор: иван171
Предмет: Українська мова,
автор: Гость2016
Предмет: Химия,
автор: kseniyaf110204