Question

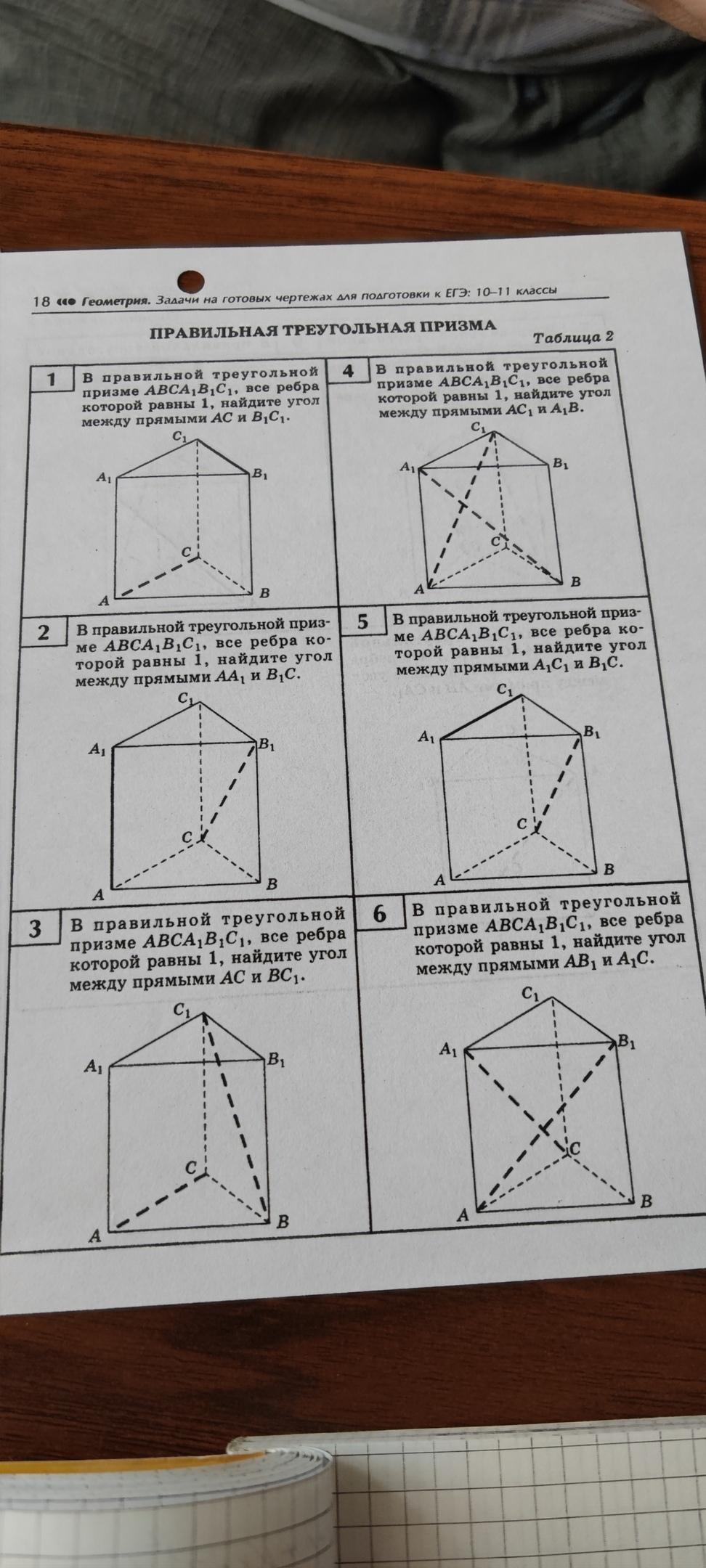
Помогите, пожалуйста, с номерами 4, 5, 6, с решением. Заранее спасибо.

Answer 1

Ответ:

Объяснение:

Угол между скрещивающимися прямыми - это угол между прямыми, параллельными заданным и лежащими в одной плоскости.

Так как все ребра равны 1 ⇒ основания призм - равносторонние треугольники, боковые грани - квадраты.

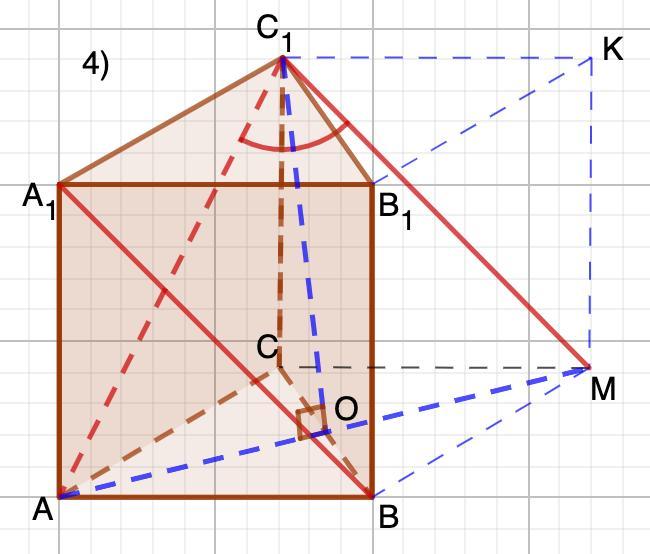
4) Достроим данную треугольную призму до четырехугольной. А₁В║С₁М. ⇒ Искомый ∠АС₁М.

По теореме Пифагора:

$AC_1=\sqrt{2} ;\;\;\;AO=\sqrt{1-\frac{1}{4} } =\frac{\sqrt{3} }{2}$

$sinAC_1O=\frac{AO}{AC_1}=\frac{\sqrt{3} }{2\sqrt{2} }=\frac{\sqrt{6} }{4}$

∠AC₁O=$arcsin \frac{\sqrt{6} }{4}= arcsin0,61$ ≈37°

⇒ ∠АС₁М ≈37°·2=74° (С₁О - высота, биссектриса равнобедренного ΔАС₁М )

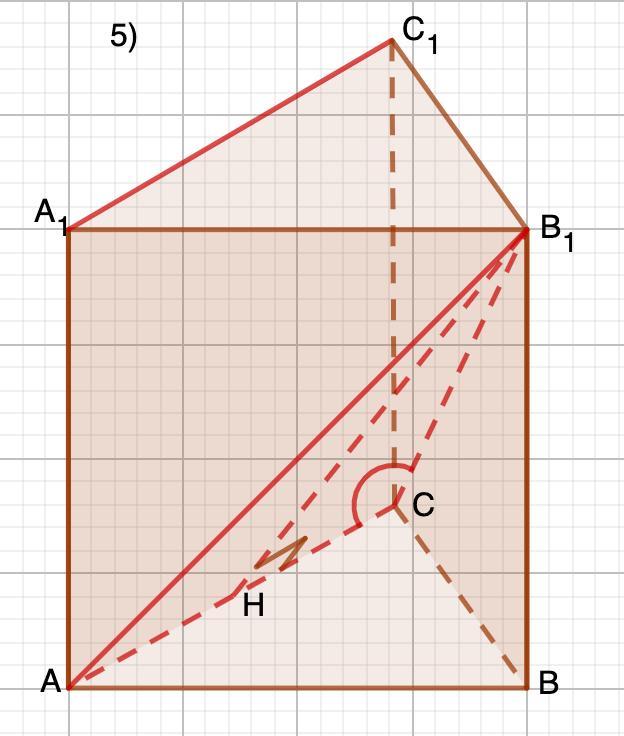
5) A₁C₁║АС ⇒ искомый ∠АСВ₁ .

По теореме Пифагора:

$AB_1=\sqrt{2}$

В₁Н - высота, медиана.

$B_1H=\frac{1}{2}$

$sinAB_1H=\frac{AH}{AB_1} =\frac{1}{2\sqrt{2} } =\frac{\sqrt{2} }{4}=0,35$

∠АВ₁Н=arcsin 0,35≈20°

⇒ ∠АВ₁С≈40° (В₁Н-высота, биссектриса равнобедренного ΔАВ₁С.)

∠В₁АС=∠АСВ₁=(180°-40°):2≈70°

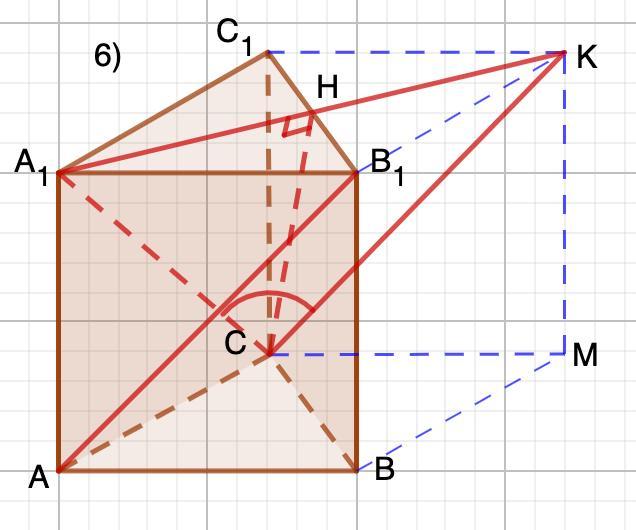
6) Достроим данную треугольную призму до четырехугольной. АВ₁║СК.

⇒ Искомый ∠А₁СК.

По теореме Пифагора:

$A_1H=\sqrt{1-\frac{1}{4} } =\frac{\sqrt{3} }{2}$

$A_1C=\sqrt{2}$

$sinA_1CH=\frac{A_1H}{A_1C}=\frac{\sqrt{6} }{4}=0,61$

⇒ ∠А₁СН=arcsin 0,61≈37°

∠А₁СК≈74° (СН-высота, биссектриса)