Предмет: Алгебра,
автор: yugolovin
Решить уравнение

Ответы
Автор ответа:
1
Ответ:
х=1
Объяснение:
очевидный корень х=1.
Докажем его единственность.
Обозначим :
y=x-1
Уравнение преобразуется в следующее :
sqrt(7y+9)+sqrt(7y+4)=sqrt(5y+9)+sqrt(5y+4)
при у больше 0 левая часть больше правой , т.к. квадратный корень функция монотонно возрастающая и sqrt(7y+9)>sqrt(5y+9) при у>0 и
sqrt(7y+4)>sqrt(5y+4) при у>0 (т.к. аргумент правой части больше аргумента левой части).
Точно также при у<0 неравенство обращается, левая часть меньше правой. Равенство достигается при у=0, что и доказывает единственность решения.
Автор ответа:
0
Ответ:
20 обязательных символов для ответа набрал
Приложения:
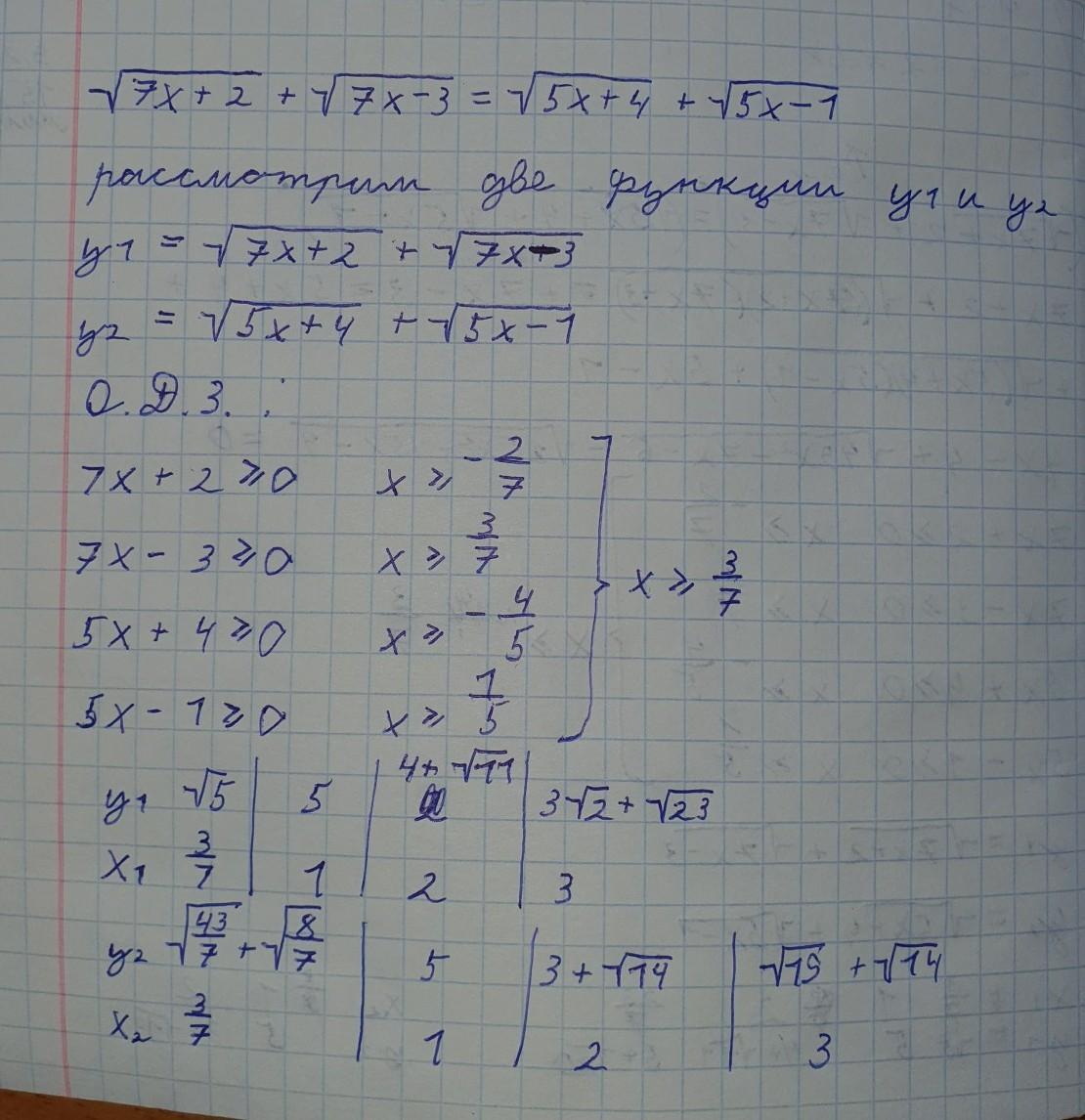
yugolovin:
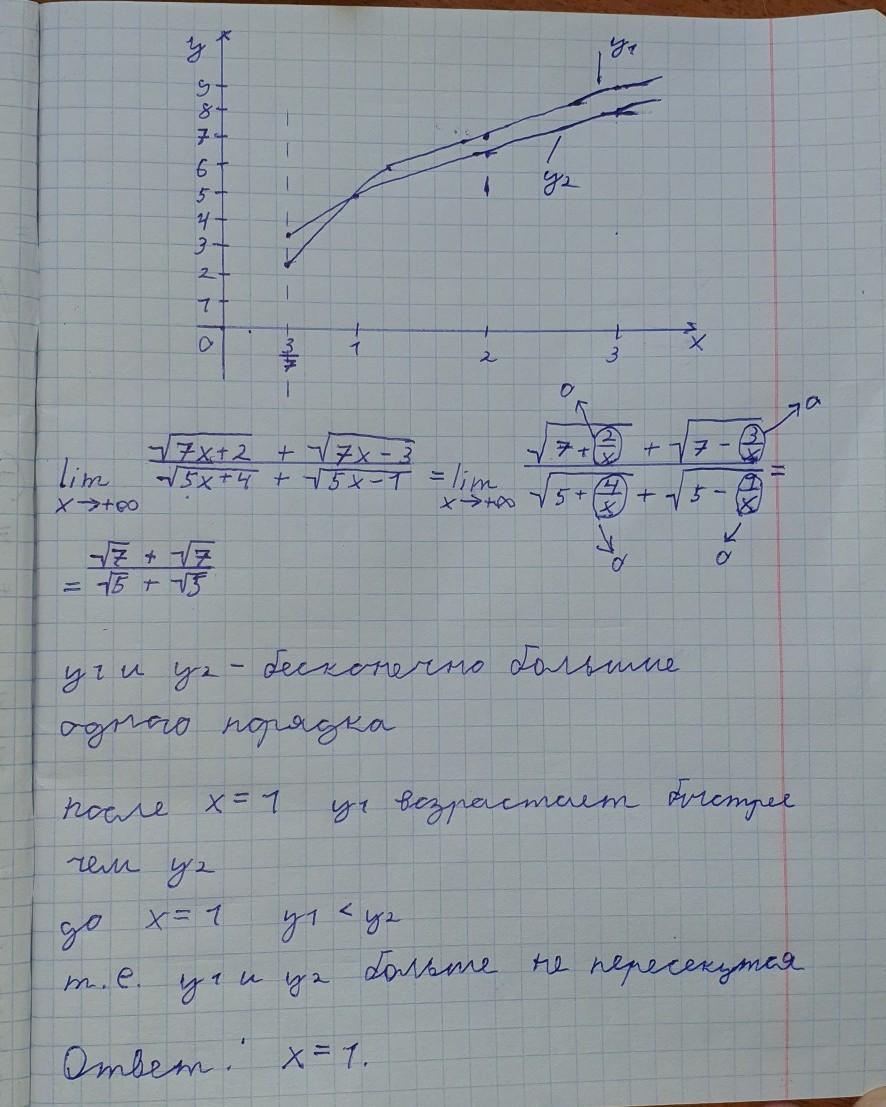
А где доказательство того, что одна функция растет быстрее другой?
Похожие вопросы
Предмет: Окружающий мир,
автор: ilyaover9000
Предмет: Українська мова,
автор: nataliasepeta
Предмет: Русский язык,
автор: Elena900
Предмет: Математика,
автор: nurai971