Question

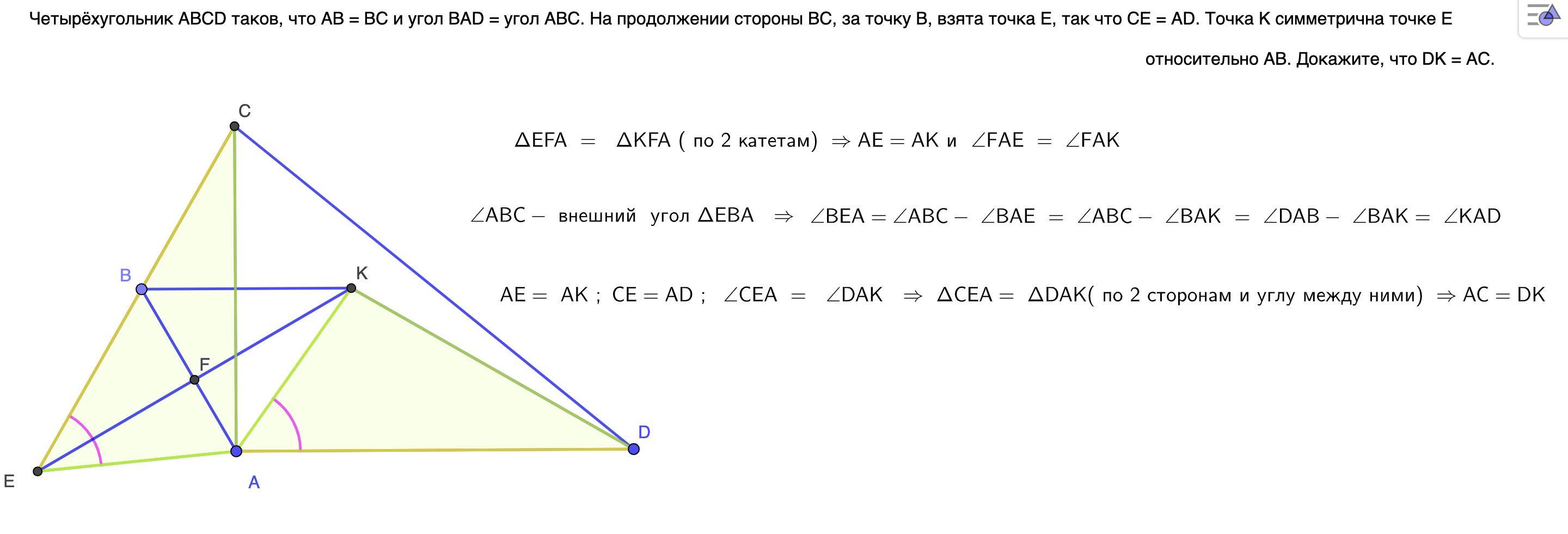
Четырёхугольник ABCD таков, что AB = BC и угол BAD = угол ABC. На продолжении стороны BC, за точку B, взята точка E, так что CE = AD. Точка K симметрична точке E относительно AB. Докажите, что DK = AC.

Answer 1

АВ = ВС -  лишнее  данное , по крайней мере в решении я это не использовал , специально сделал картинку , где это условие не выполнено  и  опять получил равные отрезки ( DK = AC)