Question

найдите сумму длин интервалов являющихся решениие неравенства

log4-x (5+x)<1

Answer 1

$log_{4-x}(5+x)<1\\----------\\ODZ\\4-x > 0\\4-x\neq 1\\5+x>0\\\\x<4\\x\neq 3\\x>-5\\\\x \in (-5;3) \cup(3;4)\\----------\\log_{4-x}(5+x)-log_{4-x}(4-x)<0$

$----------$

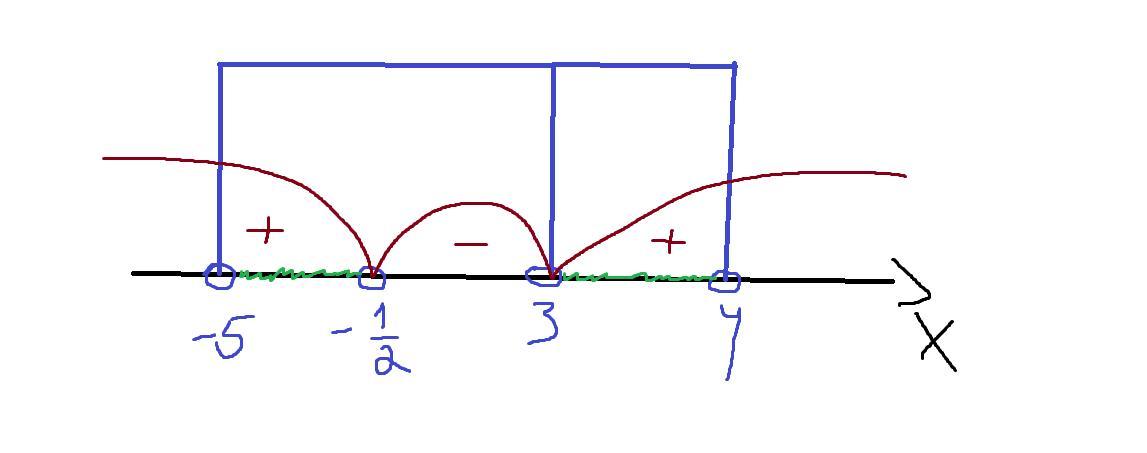
По методу рационализации функция $log_{h(x)}f(x)-log_{h(x)}g(x)$ с учетом ОДЗ принимает такие же знаки как  $(h(x)-1)(f(x)-g(x))$

$----------\\(4-x-1)(5+x-(4-x))<0\\(3-x)(2x+1)<0 |*(-\frac{1}{2})\\(x-3)(x+\frac{1}{2})>0$

(решение методом интервалов прикрепляю)

$x \in (-5;-\frac{1}{2}) \cup(3;4)$

Найдем сумму длин интервалов.

$|-5+\frac{1}{2}|+|3-4|= 4,5+1=5,5$