Предмет: Геометрия,
автор: Jikoljoni
Прямая, проходящая через точку P - середину гипотенузы АВ прямоугольного треугольника АВС, перпендикулярна СР и пересекает катет АС в точке Е. прямые РЕ и ВС пересекаются в точке М, а прямые АМ и ВЕ в точке N. Найдите NE, если СЕ : ЕА = 2:1 и BC= 4 корень из 3
Ответы
Автор ответа:
4
Ответ:
Объяснение:
Дано: ΔАВС - прямоугольный;
АР=РВ;
СР⊥КМ;
КМ∩АС=Е
РЕ∩ВС=М
АМ∩ВЕ=N
CE:EA=2:1
Найти: NE.
Решение:
Соединим точки С и N.
1. Рассмотрим ΔАВС - прямоугольный.
СР - медиана (условие)
⇒АР=РВ=РС (свойство медианы, проведенной к гипотенузе)
2. Рассмотрим ΔNMC.
MK∩AC∩NB=E
Причем, СЕ:АЕ=2:1
⇒MK;AC;NB - медианы ΔNMC.
⇒СВ=ВМ=4√3; или СВ=8√3
3. Рассмотрим ΔСРМ - прямоугольный.
РВ - медиана (п.2)
⇒РВ=СВ=ВМ=4√3 (свойство медианы, проведенной к гипотенузе)
РВ=РС=4√3 (п.1)
4. Рассмотрим ΔСРМ - прямоугольный.
5. Рассмотрим ΔЕМС - прямоугольный.
МС²=МР*МЕ (метр. соотношения в п/у Δ)
192=12*ME⇒МЕ=16
По т. Пифагора:
6. Рассмотрим ΔЕВС - прямоугольный.
ЕВ²=ВС²+ЕС²=√112
ЕВ=4√7
7. EN:EB=2:1
⇒NE=2*4√7=8√7
Приложения:
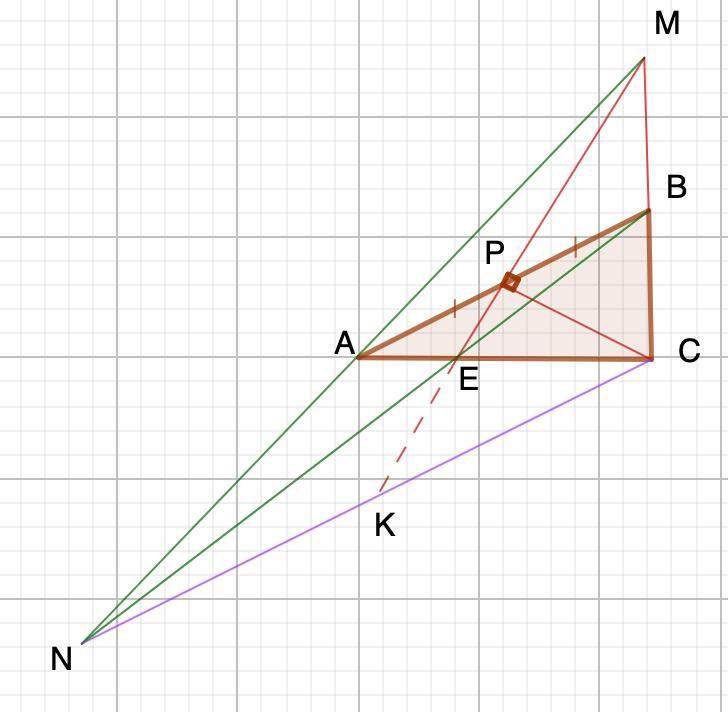
Похожие вопросы
Предмет: Русский язык,
автор: uzorggames
Предмет: Русский язык,
автор: ravganiyatbekb
Предмет: Английский язык,
автор: Аноним
Предмет: Геометрия,
автор: Alexbro696
Предмет: Математика,
автор: shilovskiyvovo