Предмет: Алгебра,
автор: yugolovin
Решите уравнение

Ответы
Автор ответа:
2
Ответ:1
Объяснение:
yugolovin:
Вот бы еще дописать "принадлежит ОДЗ"))
Автор ответа:
0
Ответ:
`1
Объяснение:
На фото
Приложения:
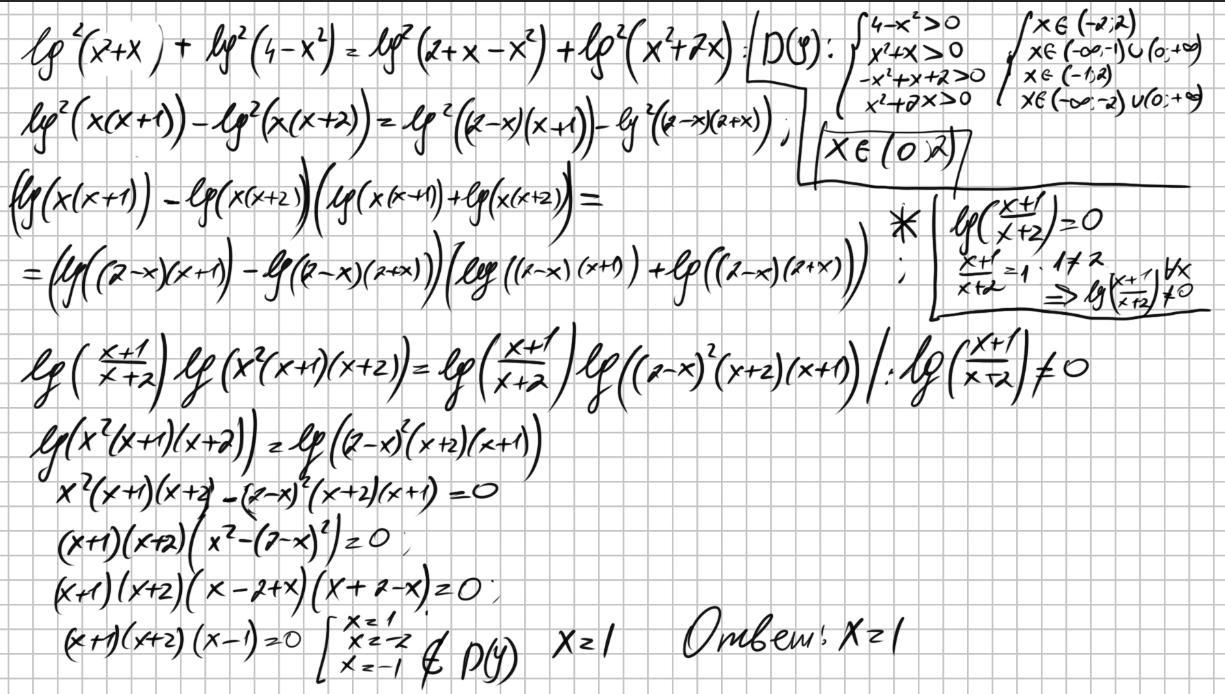
А почему lg(x+1)/(x+2) не равен нулю?
В решении под звездочкой"*" написано
Похожие вопросы
Предмет: Русский язык,
автор: Даша19февраля
Предмет: Русский язык,
автор: 170871
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: rayayakovenko
Предмет: Русский язык,
автор: Имянесуществует