Question

Помогите пожалуйста решить!!! с объяснением пожалуйста!!​

Answer 1

Ответ:

(см. объяснение)

Объяснение:

Рассмотрим сначала второе уравнение:

$\sqrt{4x-x^2}\times\sin(\pi(x-a))=0$

Произведение равно 0, когда хотя бы один из множителей равен 0, а другой при этом не теряет смысла.

Тогда:

$\left\{\begin{array}{c}\left[\begin{array}{c}\sin(\pi(x-a))=0\\x=0\\x=4\end{array}\\0\le x\le4\right\end{array}\right;$

Поработаем с первой строкой совокупности:

$\sin(\pi(x-a))=0\\\pi(x-a)=n\pi,\;n\in Z\\a=x-n,\;n\in Z$

Значит исходному уравнению равносильно:

$\left\{\begin{array}{c}\left[\begin{array}{c}a=x-n,\;n\in Z\\x=0\\x=4\end{array}\\0\le x\le4\right\end{array}\right;$

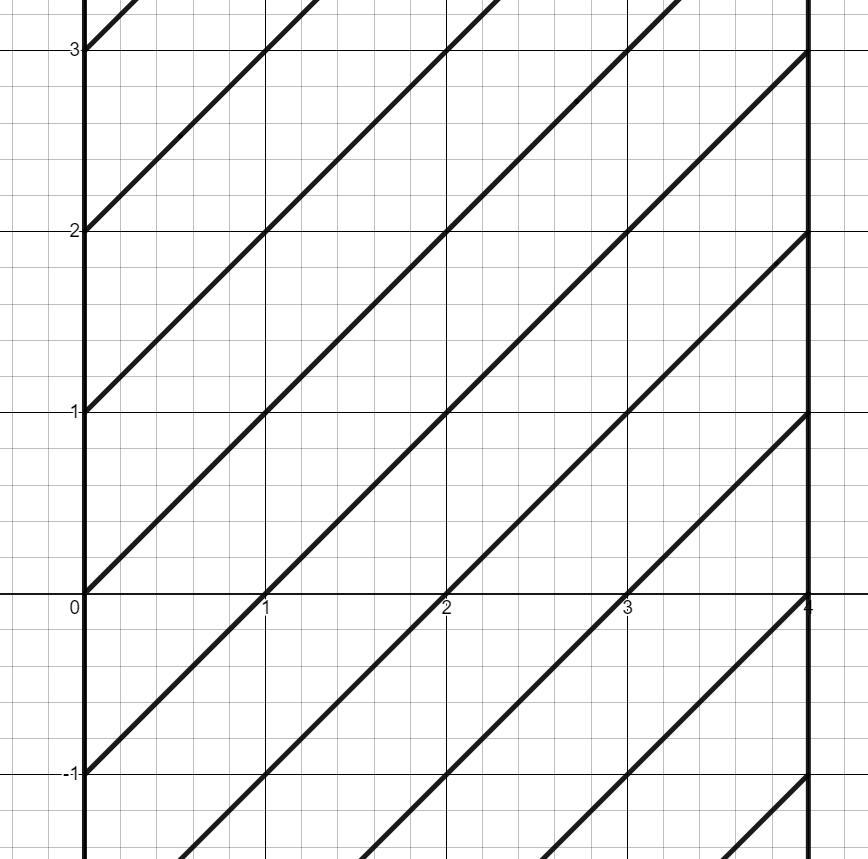
Построим записанное в координатах (x; a).

(см. прикрепленный файл)

Теперь хорошо видно, что при целых значениях параметра такое уравнение имеет ровно 5 различных корней; в другом случае их будет 6.

Рассмотрим первое из предложенных уравнений:

$\sin\dfrac{4\pi}{x^2+3x+a^2}=0$

Преобразуем его:

$\sin\dfrac{4\pi}{x^2+3x+a^2}=0\\\dfrac{4\pi}{x^2+3x+a^2}=n\pi,\;n\in Z\\\dfrac{4}{x^2+3x+a^2}=n,\;n\in Z$

Если $n=0$, это уравнение не имеет корней при любом значении параметра.

Тогда:

$x^2+3x+a^2=\dfrac{4}{n},\;n\in Z$

Здесь, если $x^2+3x+a^2=0$, то уравнение не имеет корней при любом значении параметра.

$\left(x+\dfrac{3}{2}\right)^2+a^2=\dfrac{9}{4}+\dfrac{4}{n},\;n\in Z$

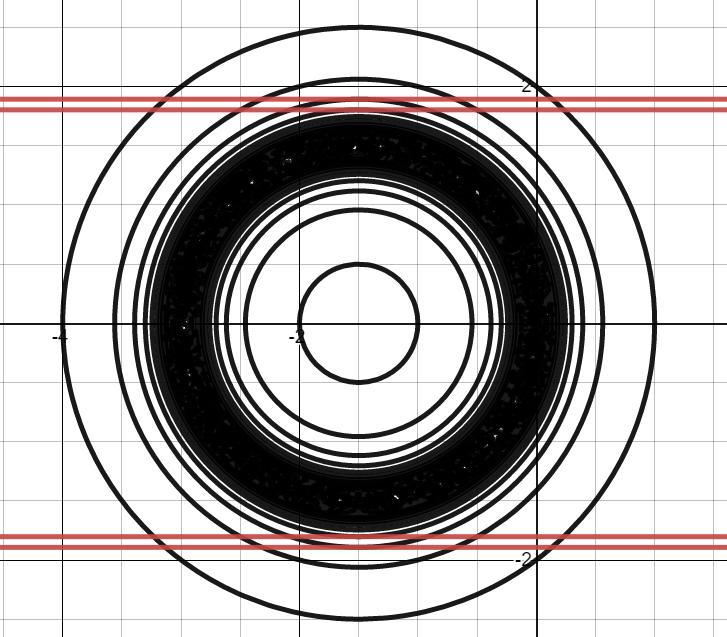
Построим записанное выше в координатах (x; a). Получится уравнение большого количества окружностей. Причем при $n=1$ будет окружность с наибольшим радиусом, а при $n=-2$ с наименьшим. Это связано с тем, что мы число 4 делим на $n$ и $n$ принадлежит множеству целых чисел. Между этими двумя окружностями будет находиться скопление других, очень близко расположенных друг к другу и практически сливающихся при выбранном мною масштабе.

Отобразим это в выбранной системе координат.

(см. прикрепленный файл)

Красными прямыми покажем удовлетворяющие нас случаи. Сразу видно, что пяти пересечений с графиком при целых значениях параметра не будет, что еще раз подтверждает верность указанного расположения.

Значение параметра - это перпендикуляр от центра окружности до прямой, то есть радиус этой окружности, поэтому просто подставляем $n=3$ и $n=4$ в выражение $\sqrt{\dfrac{9}{4}+\dfrac{4}{n}}$.

Итого при $a\in\left(-\dfrac{\sqrt{129}}{6};\;-\dfrac{\sqrt{13}}{2}\right)\cup\left(\dfrac{\sqrt{13}}{2};\; \dfrac{\sqrt{129}}{6}\right)$ число корней уравнения $\sin\dfrac{4\pi}{x^2+3x+a^2}=0$ равно числу корней уравнения $\sqrt{4x-x^2}\times\sin(\pi(x-a))=0$.

Задание выполнено!