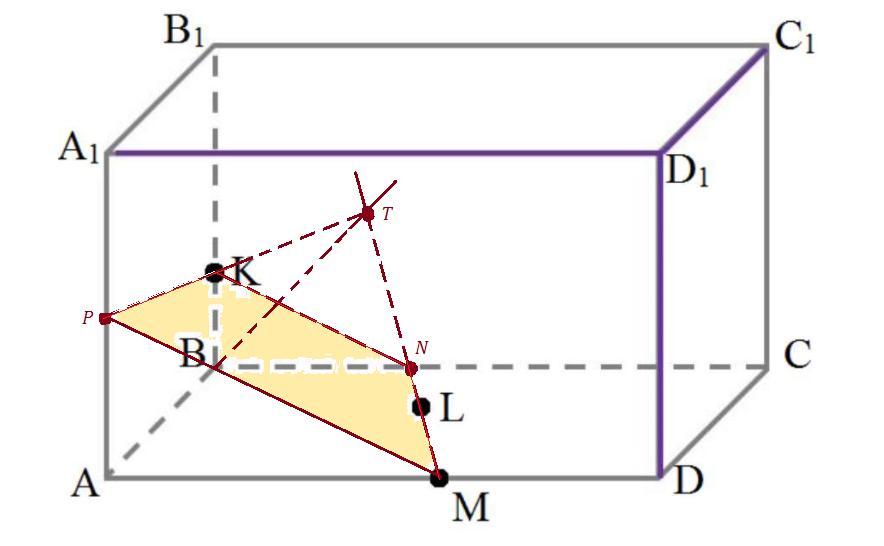
Задан прямоугольный параллелепипед ABCDA1B1C1D1. Точка K лежит на ребре BB1, точка M – на ребре AD, точка L – на нижней грани.
а) Постройте сечение параллелепипеда по 3 заданным точкам K, L, M. Объясните ход построения каждого из отрезков.
б) Укажите название (вид) полученного многоугольника и заштрихуйте его внутреннюю часть.
Ответы
Проводится отрезок через точки M и L до пересечения с ребром ВС.
Получаем точку Р.
Потом соединяем Р и К.
Далее используется свойство - в параллельных плоскостях линии сечения параллельны. Получаем точку Т.
Проводим МТ и КТ.
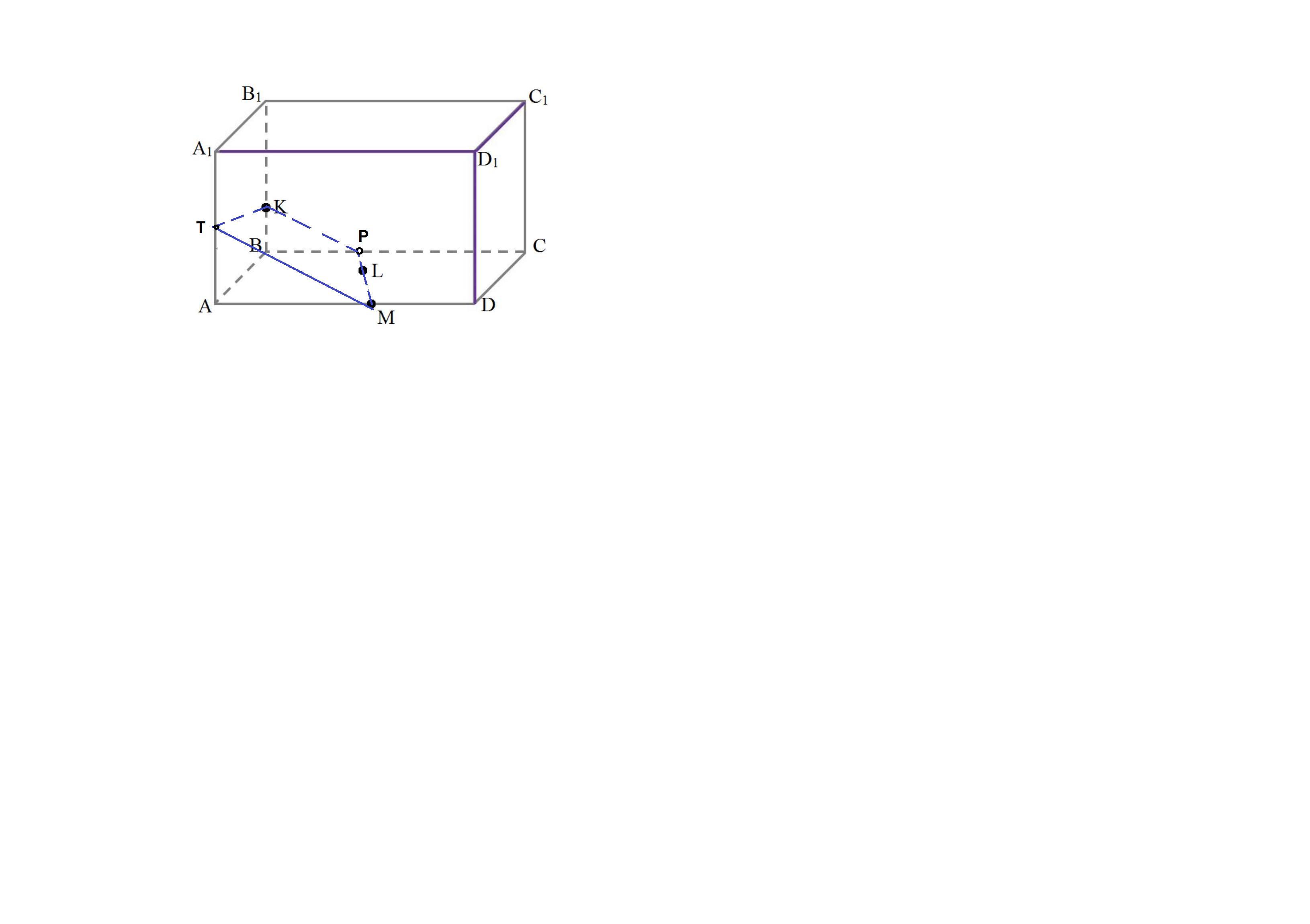
Ответ:
Соединим точки М и L , лежащие в одной плоскости ABCD . ML пересекается с ВС в точке N .
Продлим ML до пересечения с АВ , получим точку Т .
Теперь соединим точку Т и точку К , так как они лежат в одной плоскости АА1В1В . Продлим КТ до пересечения с АА1 в точке Р .
Соединим точки Р и М , так как они лежат в одной плоскости AA1D1D .
Получили сечение МNKP . Это трапеция, так как МР || KN в силу того, что если две параллельные плоскости ( АА1D1D и BB1C1C ) пересечены третьей ( MNKP ), то линии их пересечения параллельны.