Предмет: Математика,
автор: 143degctym
Помогите решить уравнение, спасибо
Приложения:

LFP:
сведется к уравнению третьей степени)) первый корень подбирается устно: х=2)) оставшееся квадратное уравнение не имеет корней (ВБ0)
Ошибся заданием, но все равно большое спасибо) Сейчас загружу то, в котором не могу найти решение
https://znanija.com/task/45127534
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Введём замену:
Перепишем уравнение с учётом замены:
Сумма первого и второго слагаемых равна 72, поэтому в выборе делителей числа 72 ограничимся следующими числами:
Разделив многочлен на t – 4, получим:
Найдём корни второго множителя.
Действительных корней нет.
Вернёмся к замене:
Приложения:
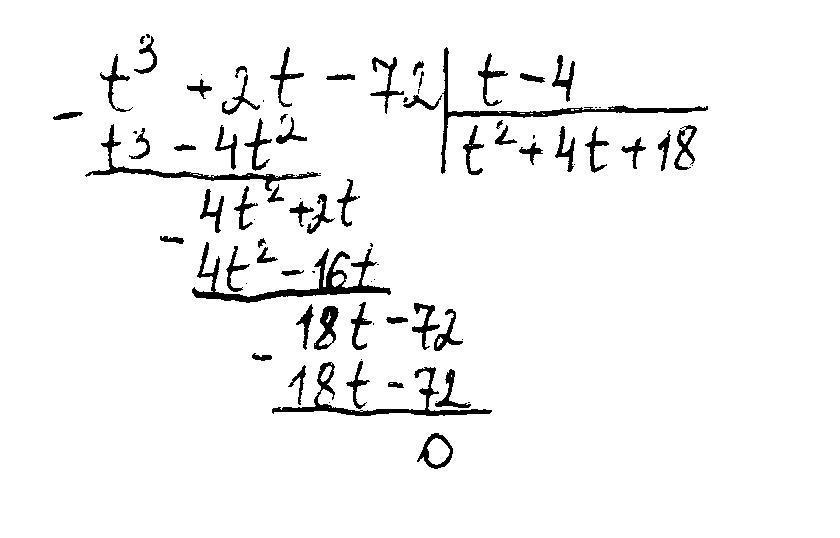
Спасибо, но тут и правда устно можно и куда короче
Пожалуйста.
https://znanija.com/task/45127534
Вот если не трудно, еще одно, но система уже
Вот если не трудно, еще одно, но система уже
Похожие вопросы
Предмет: Русский язык,
автор: Lelerara3737
Предмет: Қазақ тiлi,
автор: OWB
Предмет: Русский язык,
автор: холла1
Предмет: Биология,
автор: ggggwp1515