Предмет: Математика,
автор: Риммулька
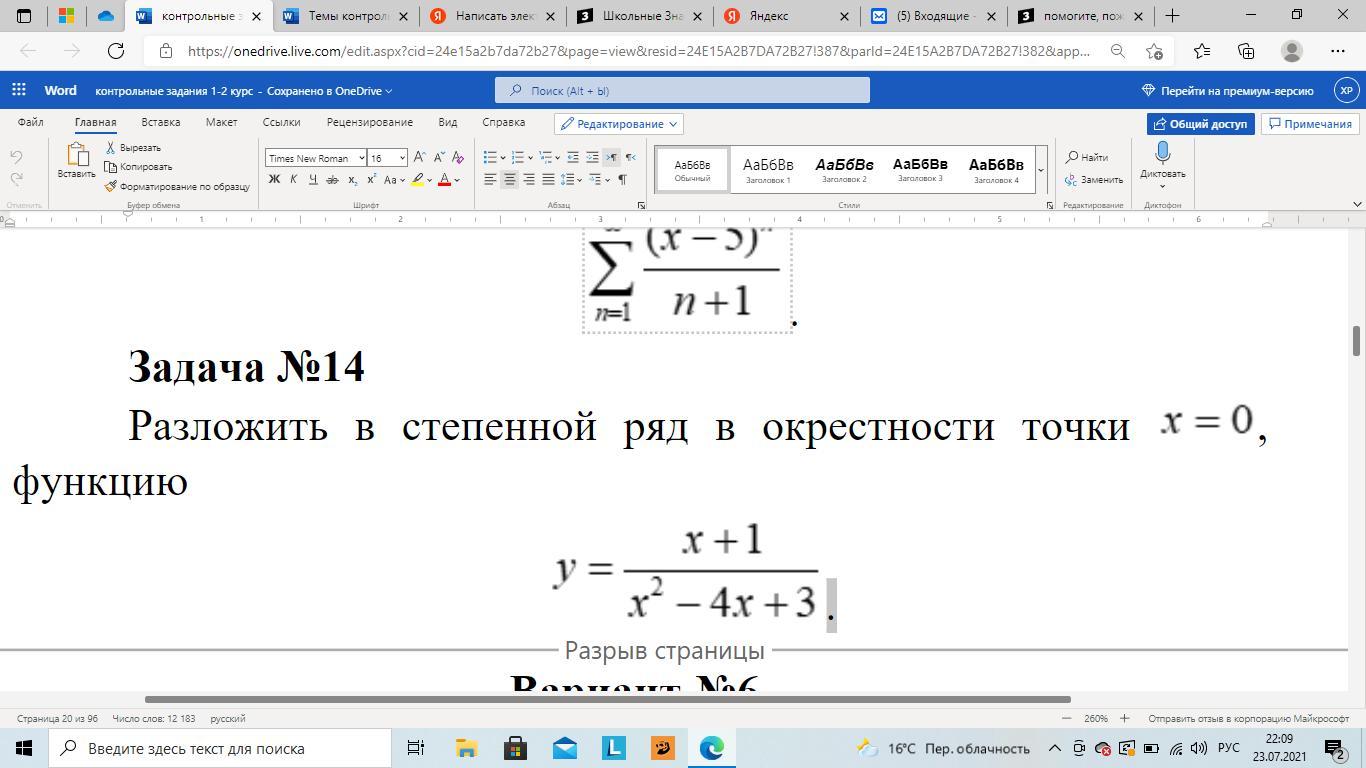
помогите, пожалуйста, решить задачу 14
Приложения:
terikovramazan:
какой порядок разложения?
дробь равна 2 / (x-3 ) + 1 /(1-x) , 1 /(1-x) = 1 +x + x^2 + ... +x^n ; 1 /(x-3) = -1/3 * 1 /(1 -x/3 ) = -1/3 ( 1 +x/3 + x^2 / 9 + .... )
Ответы
Автор ответа:
1
Ответ:
у= сумма по n a(n)*x^n n от 0 до бесконечности
a(n)=1--0,5/(3^n)
Пошаговое объяснение:
x^2-4x+3=(x-1)*(x-3)
у=1/(х-3)+2/((х-1)(х-3))=(1/(х-3)+(1/(х-3)-1/(х-1))=2/(х-3)-1/(х-1)=(-2/3) (1/(1-(х/3))+1/(1-х)
Сумма двух геометрических прогрессий.
Первая (-1/2)*(1+(х/3)+(х/3)^2+ ...)
вторая (1+x+x^2+...)
у= сумма по n a(n)*x^n n от 0 до бесконечности
a(n)=1--0,5/(3^n)
x^2-4x+3 не равно (x+1)*(x+3)
Верно, сейчас исправлю.
Похожие вопросы
Предмет: Русский язык,
автор: artspan4
Предмет: Русский язык,
автор: nadyarus
Предмет: Русский язык,
автор: kuhfxfh
Предмет: Математика,
автор: RouseMik
Предмет: Геометрия,
автор: Аська241