Предмет: Геометрия,
автор: mishjenner93
Площадь прямоугольника треугольника равна 1, а радиус описанной около него окружности равен корень 5/2. Найдите косинус острого угла между медианами данного треугольника, проведёнными к его катетам.
Ответы
Автор ответа:
2
Ответ:
Объяснение:
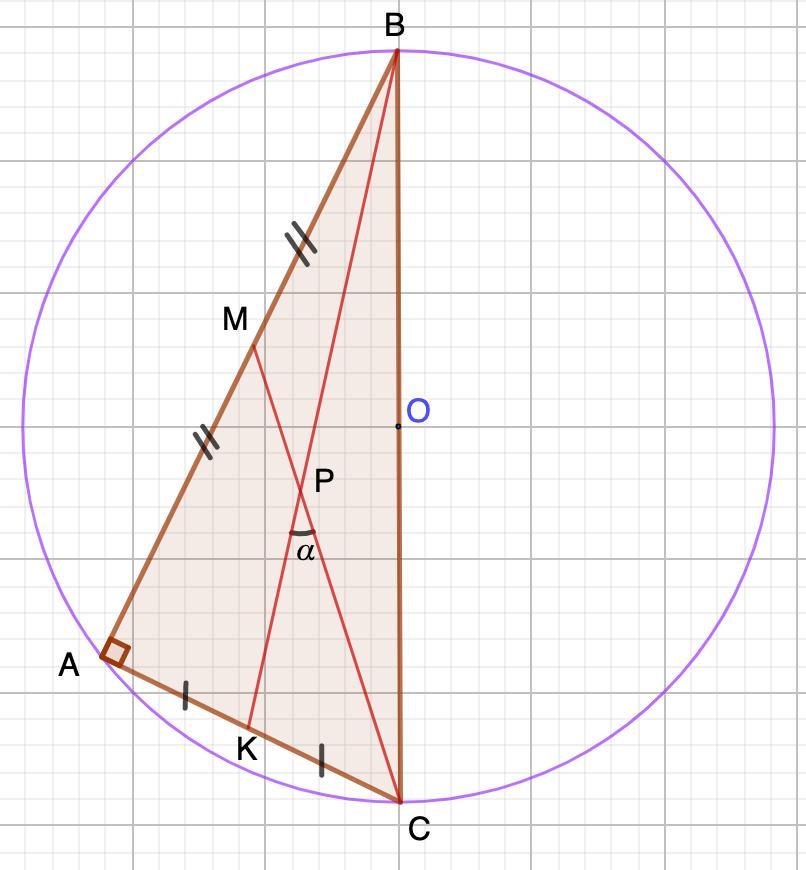
Дано: Окр.OR-описанная
ΔАВС - прямоугольный
ВК и СМ - медианы
Найти: cosα
Решение:
1. Окр. OR - описана около ΔАВС ⇒СВ - диаметр (прямой угол опирается на диаметр)
2. Рассмотрим ΔАВС - прямоугольный.
Пусть меньший катет = a, больший - b.
Тогда:
Площадь треугольника:
По теореме Пифагора:
Составим систему:
По теореме Виета:
Или
Тогда АС=1; АВ=2.
3. Рассмотрим ΔАВК - прямоугольный.
(ВК-медиана)
По т. Пифагора
(св-во пересекающихся медиан)
4. Рассмотрим Δ МАС - прямоугольный.
(СМ-медиана)
По т. Пифагора
(св-во пересекающихся медиан)
5. Рассмотрим ΔКРС
Используем теорему косинусов:
Имеем
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 15202
Предмет: Английский язык,
автор: неле4ка
Предмет: Українська мова,
автор: tarascem
Предмет: Алгебра,
автор: anton65422
Предмет: Математика,
автор: 1hochuvsharagy1