Предмет: Математика,
автор: arsbryant
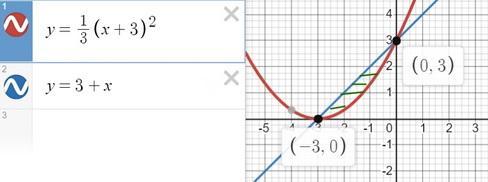
Найдите площадь фигуры, ограниченной линиями
Приложения:

Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
рисуем графики и видим фигуру, границы интегрирования, у₁ и у₂
и тогда площадь фигуры по формуле
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: 23456aaaффф
Предмет: Русский язык,
автор: мишкпц
Предмет: Русский язык,
автор: KASPIISKA
Предмет: Математика,
автор: dimin2
Предмет: Математика,
автор: zaretaboltaeva