Question

Помогите пж!!! ДАЮ 30 БАЛЛОВ!!!
В прямоугольный треугольник со сторонами 3, 4, 5 вписана окружность с центром I. Найдите расстояние от точки I до медианы, проведённой к гипотенузе треугольника.

Answer 1

Ответ 0,2.

Решение задания прилагаю

Answer 2

Вариант решения.

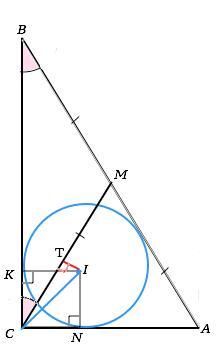
    Назовем треугольник АВС. Искомое расстояние - длина отрезка IT, проведенного из центра окружности перпендикулярно медиане.

  Центр вписанной окружности лежит на биссектрисе треугольника АВС.

r=IK =IN - отрезки, проведенные из центра вписанной окружности к точкам касания, – стороны квадрата КLNC.

 Для прямоугольного треугольника  r=(a+b-c):2

r=(3+4-5):2=1

CI=IN:sin45°=1:(√2/2)=√2  

По свойству медианы прямоугольного треугольника СМ=ВМ=АМ

∆ BМС- равнобедренный, ∠МВС=∠МСВ.

sin МСВ=sin МВС=sin АВС

sin МСВ=AC/AB=3/5=0,6

По таблице ( на калькуляторе  - точнее) находим по синусу угол МСВ=36,87°.

Биссектриса делит прямой угол на два по 45°.

∠МСI=угол ВСI-угол ВСМ=45°-36,87°=8,13°

∆ СIT- прямоугольный, CI - гипотенуза.

Катет ТI=CI•sin8,13°

TI=√2•0,1414=0,19996979…= 0,2