Предмет: Алгебра,
автор: hghyf25vhh
Только 4 и 5 ⬆️⬆️⬆️⬆️⬆️⬆️⬆️
Приложения:
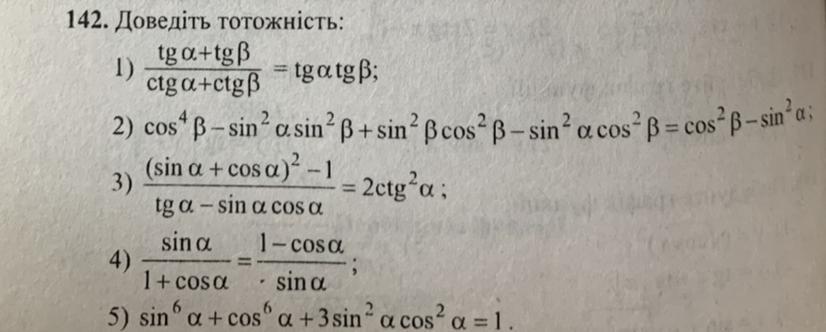
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Если разность левой и провой частей тождества равна нулю, то они равны . Тождество доказано .
Тождество доказано
Похожие вопросы
Предмет: Русский язык,
автор: ммлж
Предмет: Английский язык,
автор: nazi80289
Предмет: Русский язык,
автор: лизун7
Предмет: Биология,
автор: Anastasia200622
Предмет: Геометрия,
автор: vikakiosse092003