Предмет: Алгебра,
автор: vichkapostukh
помогите пожалуйста 7 и 8
Приложения:
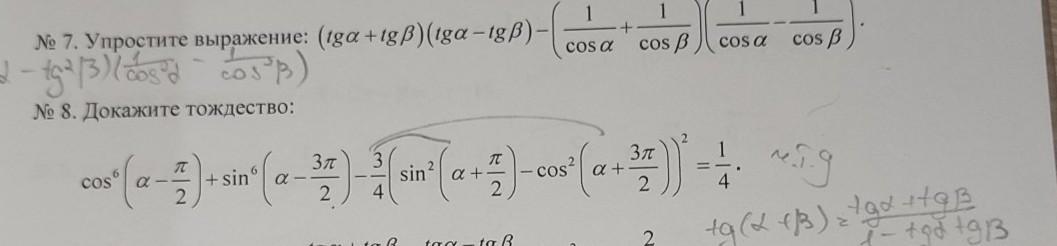
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: аквамарин51
Предмет: Русский язык,
автор: nyanyanya1
Предмет: Русский язык,
автор: andrioid
Предмет: Математика,
автор: Natali2119
Предмет: Математика,
автор: ghucicyugyik