Предмет: Геометрия,
автор: sof2626
Расстояние между точками касания со вписанной и соответствующей вневписанной окружностью треугольника ABC на стороне BC равно 2, а на стороне AC равно 3. Чему может быть равна длина стороны AC, если BC=10?
Simba2017:
сириус?
в базе есть решение, но судя по отсутствию чертежа-я бы ему не доверяла
Ну, вот я недавно уже это говорил. На стороне BC = a; точка касания с вписанной окружностью делит её на отрезки длиной p-b и p-c. Точки касания вписанной и вневписанной окружности симметричны относительно середины стороны. То есть расстояние между ними Ia - 2(p-b)I=Ib-cI (вместо p-b можно взять p-c, получится то же самое).
Ну и можно считать. IAB-ACI=2; IAB-BCI=3; BC=10. => AB = 13 или 7; если BC=10; AB=13; то AC=15 или 9; если BC=10; AB = 7; то AC=9 или 5; всего четыре варианта. Правило треугольника вроде нигде не нарушено. Ну проверьте это, можно для каждого варианта найти расстояния и сравнить с условием.
Ответы
Автор ответа:
4
Ответ:
АС=15
Объяснение:
............................................
Приложения:
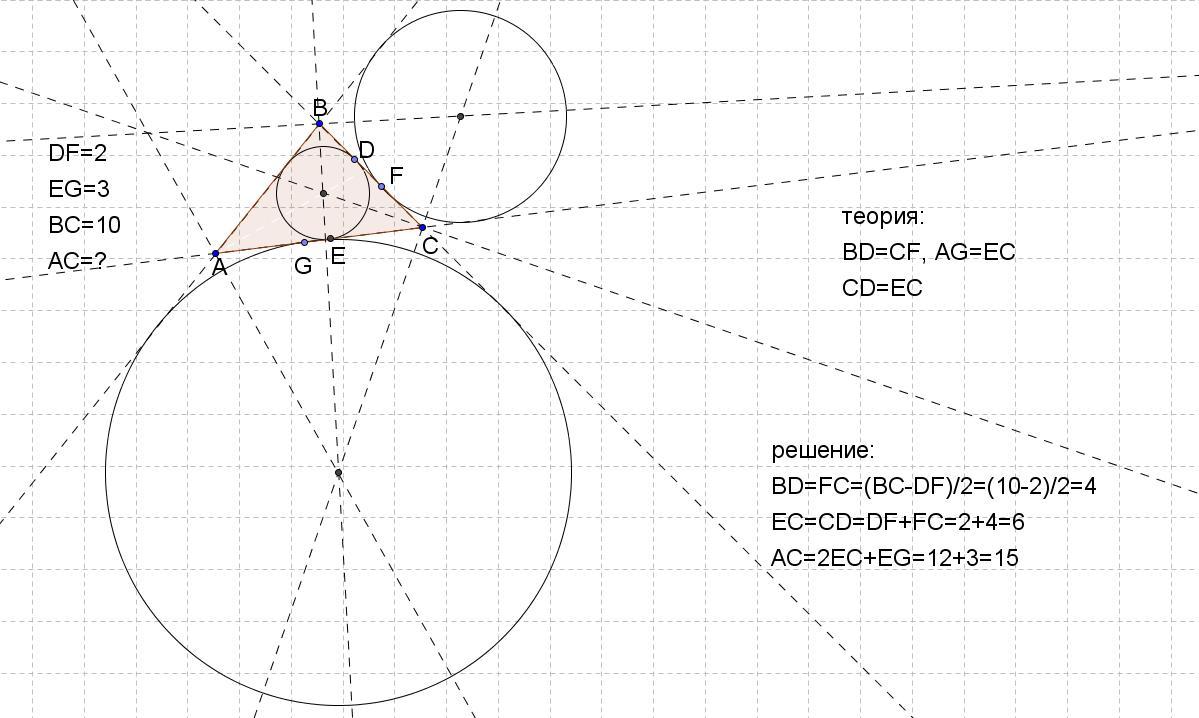
Почему вам не подошло BC=10, AB = 7, AC = 5? Отрезки касательных будут на BC 6 и 4, на AB 6 и 1, на AC 4 и 1. На BC расстояние между точками касания 2, на AC - 3. Все удовлетворено. Из тех 4 вариантов, что я привел в верхнем комментарии, кое-что не подходит, но это-то работает :)
какой ответ? чему может быть равна сторона АС?
АС=15, готового ответа не видите?!!!
Похожие вопросы
Предмет: Русский язык,
автор: tata12341
Предмет: Русский язык,
автор: yaanna230121
Предмет: Русский язык,
автор: dacha951
Предмет: Информатика,
автор: mgghjbb
Предмет: Математика,
автор: Solt369