Предмет: Алгебра,
автор: Sanya21Century
Помогите, пожалуйста, срочно!!!
Приложения:
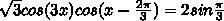
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Объяснение:
Уравнение решено!
Sanya21Century:
ты лучший
а кстати, такой вопрос, мне не понятно как ты объединил в систему уравнения после 3 строчки и приравнял к одному, объясни пожалуйста
типо каждый из них равен по одному и в сумме дают 2 судя по третьей строчке?
А какой случай еще вы видите?
Наибольшее значение косинуса какое?
ну просто не сразу дошло, типо обычно в таких задачах постоянно к 0 приравнивают, но здесь исключение
Такое я очень часто встречаю. Запоминайте прием, он поможет.
спасибо!!!
Похожие вопросы
Предмет: Русский язык,
автор: stremyakovayuliya
Предмет: Русский язык,
автор: татьяна85
Предмет: Английский язык,
автор: тонна2
Предмет: Английский язык,
автор: kavai2girl
Предмет: Русский язык,
автор: Lester123