Пожалуйста, решите срочно матан
Найти сумму координат точки
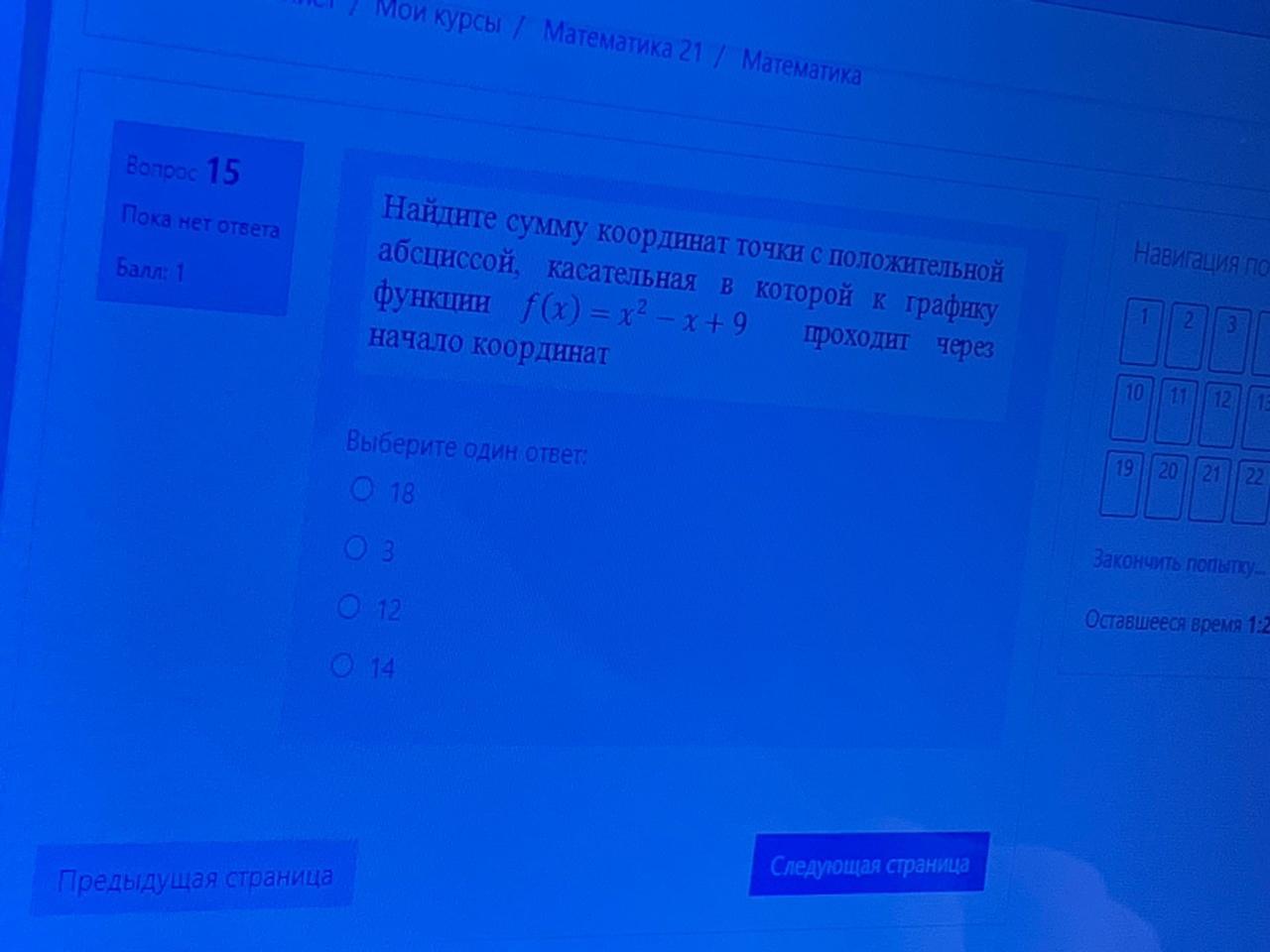
Ответы
Ответ:
18
Пошаговое объяснение:
уравнение касательной
у нас
запишем наше уравнение касательной
теперь мы знаем, что касательная должна проходить через точку (0;0),
т.е.
подставим это в уравнение касательной
решим это уравнение относительно х₀
итак, у нас есть две точки касания, касательные в которых проходят через точку (0; 0). но по условию нам нужна только точка с положительной абсциссой, поэтому наше решение х₀ = 3 и точка имеет координаты
f(3) = 3² -3 +9 = 15 и тогда точка (3; 15)
и тогда сумма координат 3 +15 = 18 - это уже ответ.
но мы дополнительно найдем уравнение касательной, чтобы проверить наш ответ
подставим это значение в уравнение касательной (1)
это и есть уравнение касательной с положительной абсциссой и проходящей через начало координат
и тогда наш
ответ
3 + 15 = 18
