Question

Трапеция ABCD с основаниями AD - 27 и BC - 12 имеет равные углы ABC и ACD. Найдите длины диагонали AC и боковых сторон,
если периметр трапеции равен 64.

Answer 1

Ответ:

AC=18; AB=10; CD=15

Объяснение:

Дано: Трапеция ABCD.

AD и BC - основания.

AD=27; BC=12.

∠ABC=∠ACD.

P трапеции =64.

Найти: AC; AB; CD.

Решение:

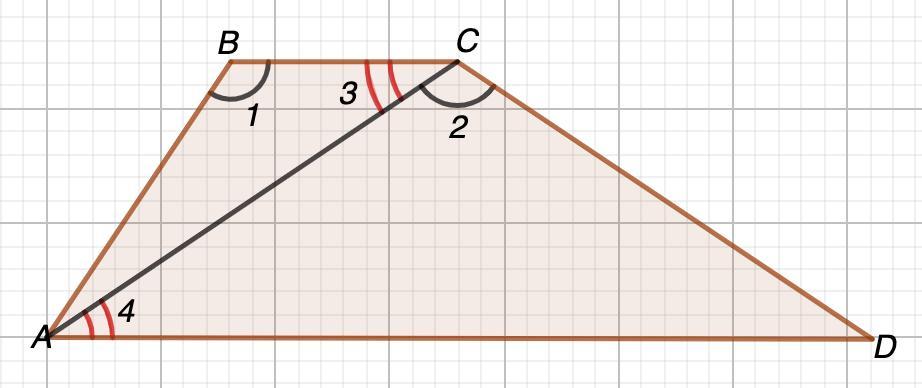
1. Рассмотрим ΔABC и ΔACD.

∠1=∠2 (по условию)

∠3=∠4 (накрест лежащие при BC║AD и секущей AC)

⇒ΔABC ~ ΔACD (по двум углам)

2. Составим пропорцию:

$\frac{BC}{AC}=\frac{AC}{AD}\\AC^2=BC*AD\\AC^2=12*27=324\\AC=18$

3. Составим еще одну пропорцию:

$\frac{AB}{CD}=\frac{AC}{AD}\\\frac{AB}{CD}=\frac{18}{27}=\frac{2}{3}$

4. Зная периметр трапеции, можем найти сумму боковых сторон:

$AB+CD=64-BC-AD=64-12-27=25$

5. Пусть AB=2x, тогда CD=3x.

Составим уравнение:

$2x+3x=25\\5x=25\\x=5$

⇒AB=2x=10; CD=3x=15