Предмет: Математика,
автор: hmelyqimc
решите уравнение, в ответ запишите количество корней на отрезке [0;2pi]
Приложения:
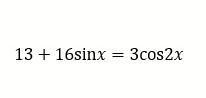
Ответы
Автор ответа:
0
Ответ:
1 корень на отрезке [0;2pi] (3pi/2)
Приложения:

Автор ответа:
1
Поэтому:
Пусть
отсюда:
Делим обе части равенства на 2:
очевидно, что:
с учётом ОДЗ:
производим обратную замену:
Это частный случай
на отрезке [0;2π] находится только 1 корень:
Похожие вопросы
Предмет: Русский язык,
автор: vickayaJamka
Предмет: Окружающий мир,
автор: REVOLUTiON11
Предмет: Русский язык,
автор: Magomed0047
Предмет: Геометрия,
автор: Ромашка7865
Предмет: Математика,
автор: yanushkevich124