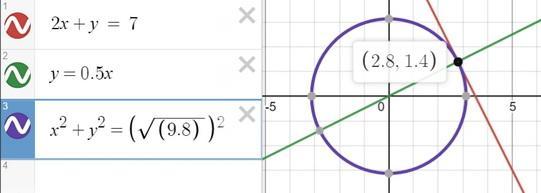Решить две задачи (во вложении). Подробно, пожалуйста

Ответы
Ответ:
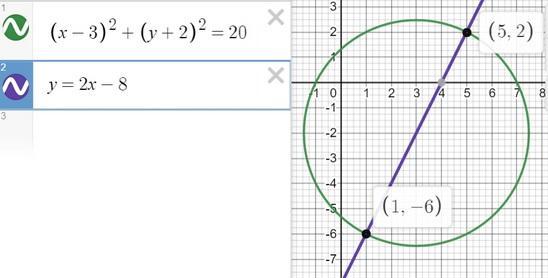
(1; -6) и (5; 2)
_______________
a = 7 / √5; (2,8; 1,4)
Пошаговое объяснение:
Преобразуем уравнение окружности так, чтобы оно приняло стандартный вид (x-b)²+(y-c)² = R², где (b, c) — координаты центра окружности, R — ее радиус:
x²+y²-6x+4y = 7
(x²-2·3x+3²)+(y²+2·2y+2²) = 7+3²+2²
(x-3)²+(y+2)² = 20
Получили, что прямая y = 2x+4a проходит через точку (3; -2). Подставим эти координаты в уравнение и найдем отсюда a:
-2 = 2·3+4a
-2 = 6+4a
4a = -8
a = -2
Стало быть, прямая задана уравнением y = 2x-8.
Координаты точек пересечения прямой и окружности удовлетворяют уравнению как прямой, так и окружности. Оставшиеся действия состоят в решении системы:
x²-6x+5 = 0. По теореме Виета:
Если x = 1, то y = 2·1-8 = -6
Если x = 5, то y = 2·5-8 = 2
Итак, заданные прямая и окружность пересекаются в двух точках: (1; -6) и (5; 2).
_______________________________
Если окружность касается прямой, то эти фигуры имеют только одну общую точку. Соответственно, и система из уравнений окружности и прямой имеет единственную пару решений.
Эта система будет иметь единственную пару решений только в том случае, когда квадратное уравнение 5x²-28x+(49-a²) = 0 будет иметь единственный корень. То есть когда его дискриминант будет равен нулю.
D = b²-4ac = (-28)²-4·5·(49-a²) = 784-980+20a² = 20a²-196
D = 0 ⇒ 20a²-196 = 0, 20a² = 196, a² = 196/20, a = 14 / √20 = 7 / √5 (отрицательный корень не учитываем, так как a здесь обозначает радиус, а он, естественно, положительный)
Стало быть, лишь при одном значении параметра окружность касается прямой. Найдем координату точки касания (подставим найденное значение a):
25x²-140x+196 = 0
D = 0
x = -b/2a = 140/(25·2) = 2,8
Тогда y = 7-2·2,8 = 1,4
Итак, координаты точки касания — (2,8; 1,4).
Ответ:
Пошаговое объяснение:
1)
приведем уравнение окружности к каноническому виду
x² +y² -6x +4y = 7
(x²-6x +9) + (y² +4y +4)^2 = 7+9+4
(x-3)² +(y+2)² =20
вот у нас уравнение окружности с центром в точке (3; -2)
теперь мы можем найти а в уравнении y = 2x+4a
раз эта прямая проходит через точку (3; -2), то и подставим эти координаты в уравнение
-2 = 2*3 +4а 4а = -2 -6 а = -2
тогда у нас будет уравнение прямой y = 2x- 8
теперь надо найти точки пересечения, т.е. надо решить систему уравнений
из первого подставим во второе
(x-3)² + (2x-8+2)² = 20
x² -6x +9 + 4x² -24x + 36 = 20
5x² +30x +25 = 0
x₁ = 1 y₁ = 2*1 - 8 = -6
x₂ = 5 y₂ = 2*5 - 8 = 2
это и есть точки пересечения прямой и окружности (1; -6) и (5; 2)
2)
касательная всегда перпендикулярна радиусу
найдем уравнение прямой, проходящей через точку (0; 0) перпендикулярно прямой 2х + у = 7 или у = 7 - 2х у этой прямой коэффициент угла наклона к = -2
формула уравнения прямой через точку (х₁; у₁) перпендикулярно
прямой у = кх +b
y - y₁ = (-1/k)(x - x₁)
подставим наши значения и получим
у = (1/2)х = 0,5х
и вот теперь найдем координаты точки касания
0.5x = 7-2x 2.5x = 7 x = 2.8 тогда у = 7 - 2*,28= 1,4
точка касания (2,8; 1,4)
а вот теперь мы можем найти радиус. это будет расстояние между центром и точкой касания
таким образом
первые графики к № 1
вторые графики к № 2