Question

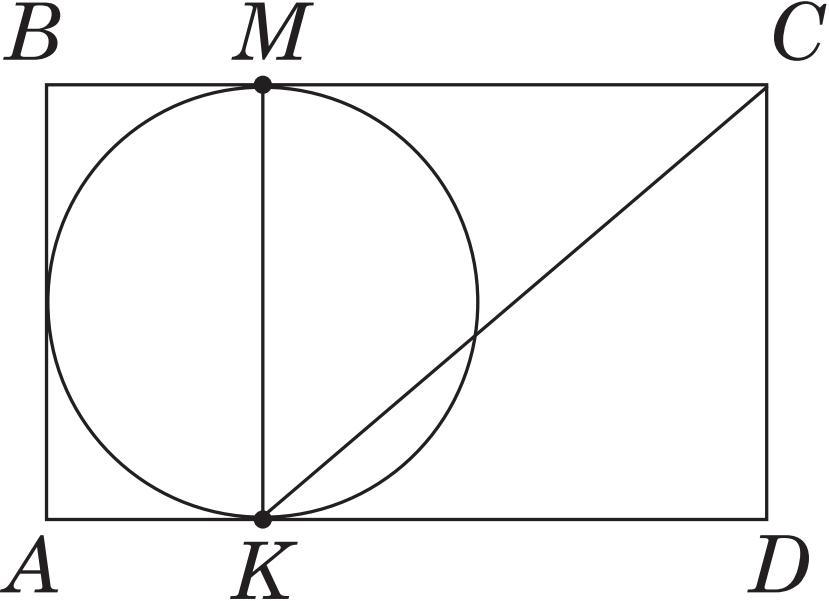
№22. На рисунке изображен прямоугольник ABCD и круг, который примыкает к стороне AB и сторон BC и AD в точках M и K соответственно. Периметр четырехугольника ABMK равен 24 см, а длина отрезка KC – 17 см.
1. Определите радиус (в см) заданного круга.
2. Рассчитайте площадь (в см²) прямоугольника ABCD.
*Ответ записывайте только десятисной дробью, учтя положение запятой.

Answer 1

Ответ:

4, 152

Объяснение:

P (ABMK) =24 = 2*BM + 2 MK = 2R+4R = 6R

(BM = R окр, MK = Dокр =2R)

6R=24, значит R = 4

MK = 8, KC =17

По т. Пифагора найдём MC

MC²+KM²=ĶC²

MC²= KC²-KM²

MC =15

BC = 15+4 = 19

AB = 8

S (ABCD) = 8×19 = 152

Answer 2

1. Пусть радиус окружности равен х см. Тогда МК = 2х, а ВМ = х. Периметр четырехугольника АВМК Р=2(ВМ+МК)=2(х+2х)=6х, равной 24 см по условию. Поэтому 6х=24, откуда х=24:6=4 см.

2. МК=2х=2*4=8 см. Из прямоугольного треугольника КМС по теореме Пифагора имеем:

KC²=KM²+MC²

172=82+MC²

289=64+MC²

MC²=289-64

MC²=225

MC=15 (см)

ВМ=4 см. Тогда ВС=ВМ+МС=4+15=19 см. АВ=МК=8 см. Площадь прямоугольника ABCD S=АВ*ВС=8*19=152 см².