Изобразить на плоскости множество точек М(x,y), для которых выполняются неравенства и вычислить его площадь.
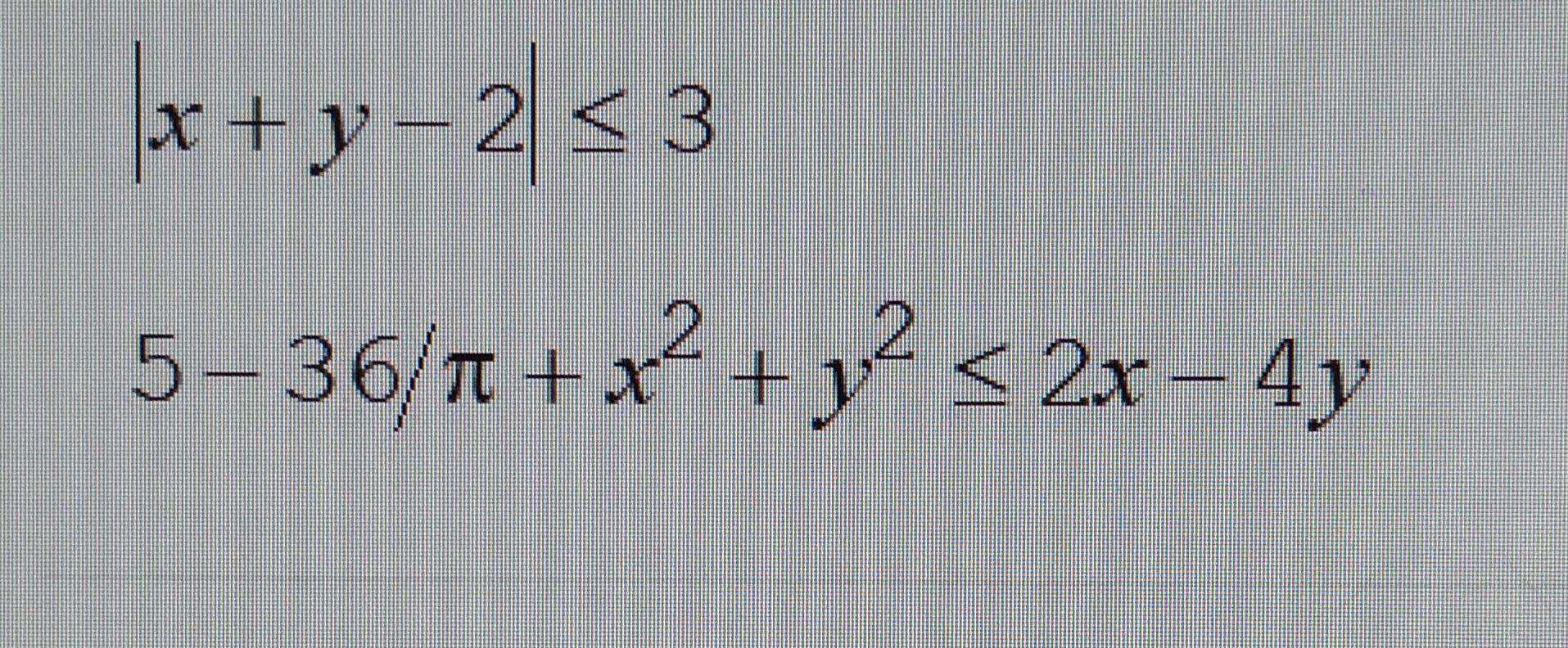
Ответы
Ответ:
Объяснение:
сначала разберемся с первым уравнением
|x + y - 2| ≤ 3
распишем его на два уравнения
х + у -2 ≤ 3 ⇒ у = 5-х
х + у - 2 ≥ -3 ⇒ у = -1 - х
нарисуем эти графики
площадь между ними и есть место точек, для которого выполняется неравенство |x + y - 2| ≤ 3
теперь второе уравнение
5 - 36/π +x² +y² ≤ 2x-4y
(x² -2x + 1) + (y² +4y +4) ≤ 36/π
(x-1)² +(y+2)² ≤ 36/π
мы тут имеем круг с центром (1; -2) и радиусом R² = 36/π
это место точек, для которых выполняется неравенство
5 - 36/π +x² +y² ≤ 2x-4y
теперь по графику мы видим, что y = -1 -x проходит через центр круга
проверим -2 = -1 -1 -2=-2
и вот мы получили, что нам надо найти площадь половины круга
ответ
площадь множества указанных точек равно 36 условных единиц
на графике:
наклонная широкая полоса наиболее темная - это место точек для функции
красный круг - это место точек для функции
